Question

помогите пожалуйста​

Answer 1

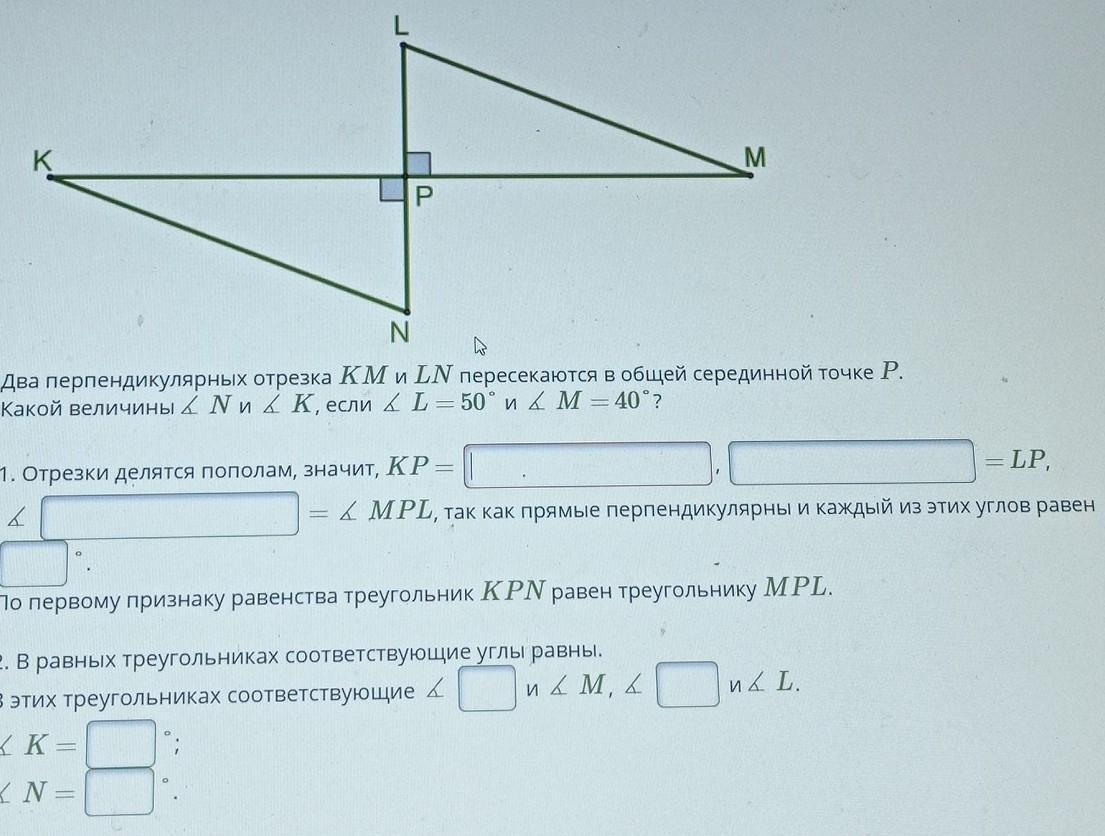
Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P.

Найти величину ∠K и ∠N, если ∠L = 50°, ∠M = 40°.

1) Отрезки делятся пополам, значит, KP = PM, PN = LP (точка P делит отрезки KM и LN на равные между собой части); ∠KPN = ∠MPL (вертикальные), так как прямые перпендикулярны и каждый из этих углов равен 90°.

По первому признаку равенства ΔKPN = ΔMPL (по двум сторонам и углу между ними; угол ∠KPN = ∠MPL; KP = PM, PN = LP).

В равных треугольниках соответствующие углы равны.

2) В этих треугольниках соответствующие углы ∠K и ∠M, ∠N и ∠L (совпадают при наложении).

∠K = 40° (Т.к. по усл. ∠M = 40°)

∠N = 50° (Т.к. по усл. ∠L = 50°)