Ответы
Ответ дал:
0
Ответ:
см
Объяснение:
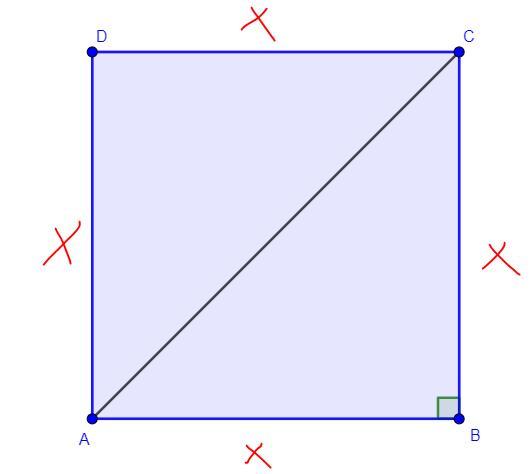
Дано: ABCD - квадрат, см
Найти: - ?
Решение: Пусть сторона AB равна x. Так как по условию ABCD - квадрат, то по свойствам квадрата все его стороны равны, следовательно AD = DC = CB = AB = x. По свойствам квадрата все его углы равны 90°. Рассмотрим прямоугольный треугольник ΔABC(∠ABC = 90°). По теореме Пифагора:
см
Так как все стороны квадрата равны, то см
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад