Question

На сторонах AB, BC и CA равностороннего треугольника ABC отмечены точки L, M и N так, что LM параллельно AC и MN параллельно AB. Докажите, что точка M и середины отрезков BN и CL являются вершинами равностороннего треугольника.

Answer 1

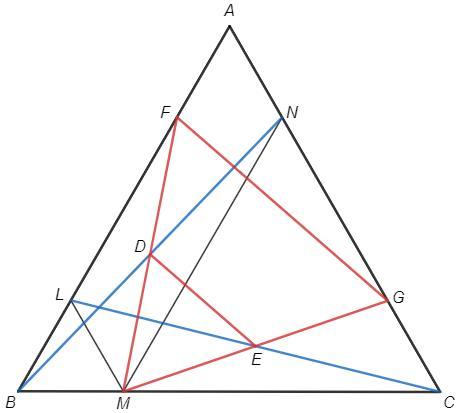
△BLM~△ABC (по соответственным углам) => △BLM - равносторонний

BL=LM=BM =t

ALMN - параллелограмм (противоположные стороны параллельны)

LM=AN =t

Отметим точки F и G, AF=CG =t

Сторона △ABC =a

BF=AG=CM =a-t

△BFM=△AGF=△CMG (по двум сторонам и углу между ними)

MF=FG=GM, △MFG - равносторонний

FN||BC (обратная т. о пропорциональных отрезках)

FBMN - параллелограмм (противоположные стороны параллельны)

D - середина BN => D - середина MF (диагонали параллелограмма)

Аналогично E - середина MG

DE - средняя линия в △MFG, DE||FG

△MDE~△MFG (по соответственным углам) => △MDE - равносторонний