Question

Установите соответствие между неравенствами и множеством его решений​

Answer 1

Ответ:

См. рисунок

Объяснение:

Нужно знать:

1) (a-b)² = a²-2·a·b+b².

2) (a-b)² ≥ 0 при любых a∈R и b∈R, (a-b)² = 0 тогда, когда a=b.

Решение.

Так как

x²-10·x+25 = x²-2·x·5+5² = (x-5)² ≥0,

то

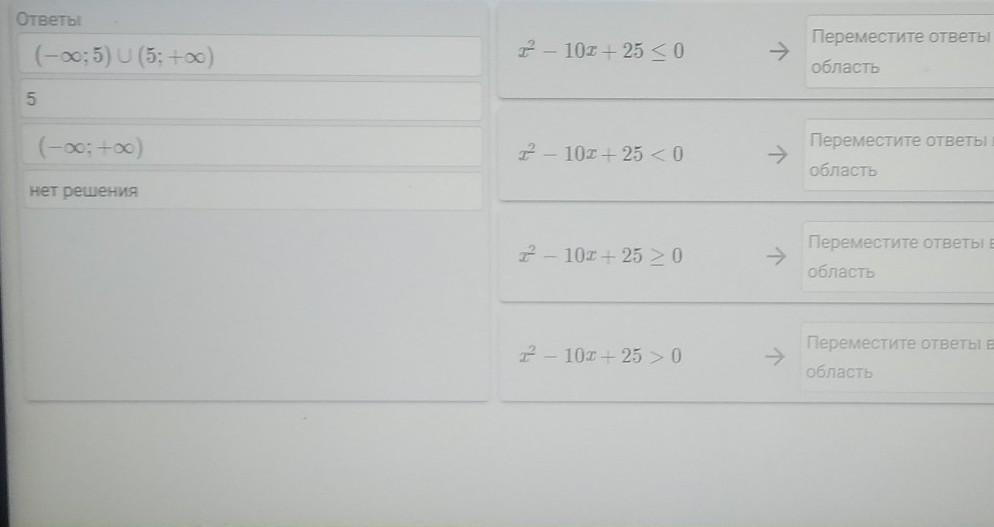
а) x²-10·x+25 ≥ 0 при любом x, то есть при x∈(-∞; +∞);

б) x²-10·x+25 > 0 при любом x кроме 5, то есть при x∈(-∞; 5)∪(5; +∞);

в) x²-10·x+25 < 0 ни при каком x, то есть нет решения;

г) x²-10·x+25 ≤ 0 выполняется только равенство при x=5.