Question

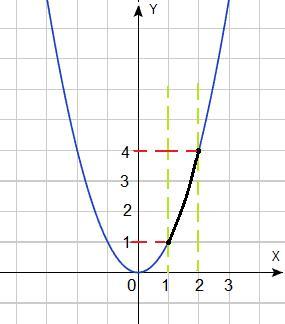
Используя выделенную часть графика y = x2 на рисунке, найди наибольшее и наименьшее значения функции y = x2, если x [1;2].
y наибольшее = ; y наименьшие = даю 10 баллав

Answer 1

$y=x^2;\ \ \ x\in[1;2]$

Функция квадратичная, ветви направлены вверх $(a=1>0).$

Вершина параболы в точке $(0;0).$

На промежутке [1;2] функция монотонно возрастает. Наименьшее значение функции на левой границе, а наибольшее значение функции на правой границе отрезка.

x = 1;    y = 1² = 1   -  наименьшее значение функции на промежутке.

x = 2;   y = 2² = 4  -  наибольшее значение функции на промежутке.

Ответ: у наибольшее = 4;  у наименьшее = 1.