Question

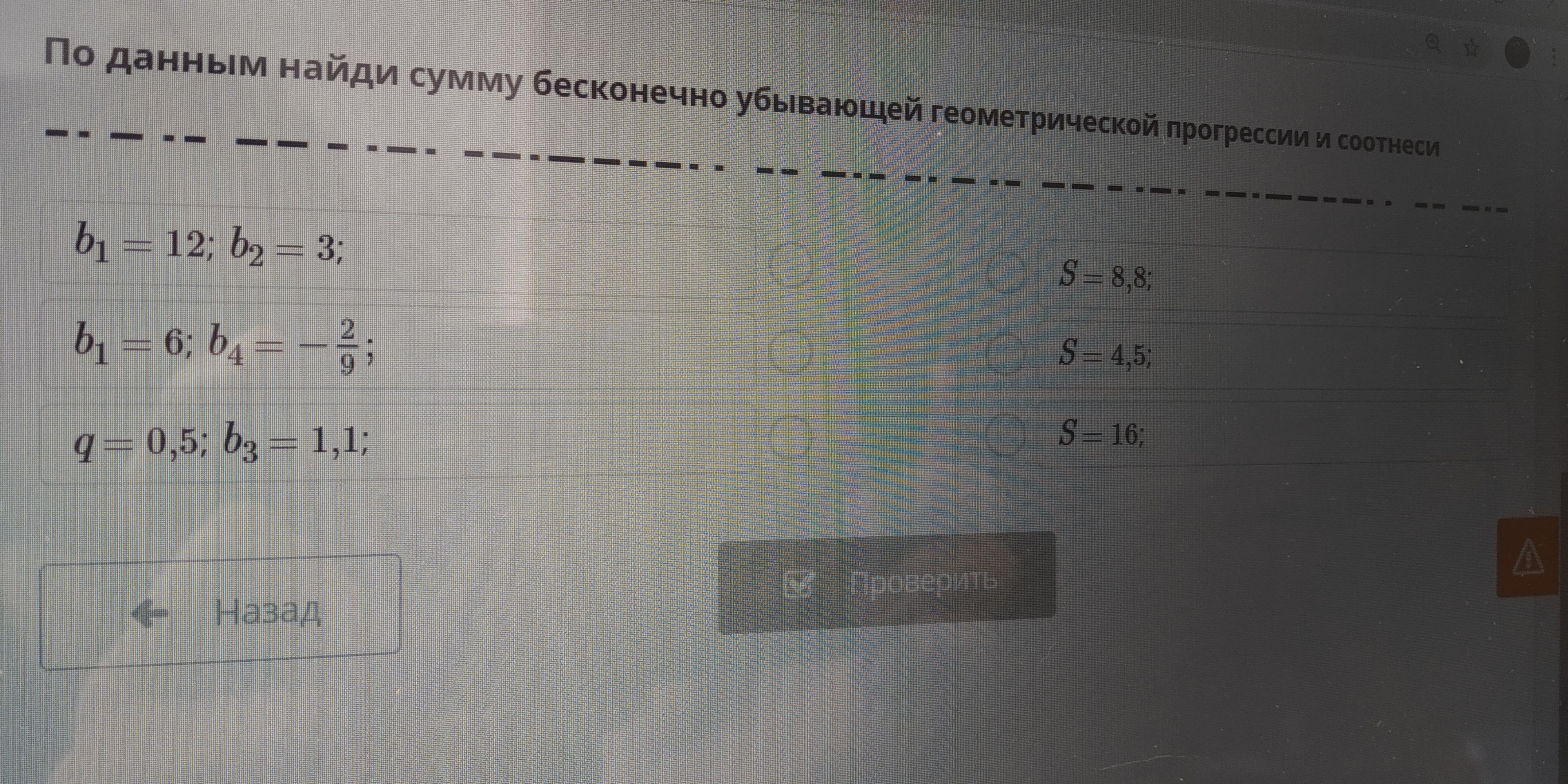
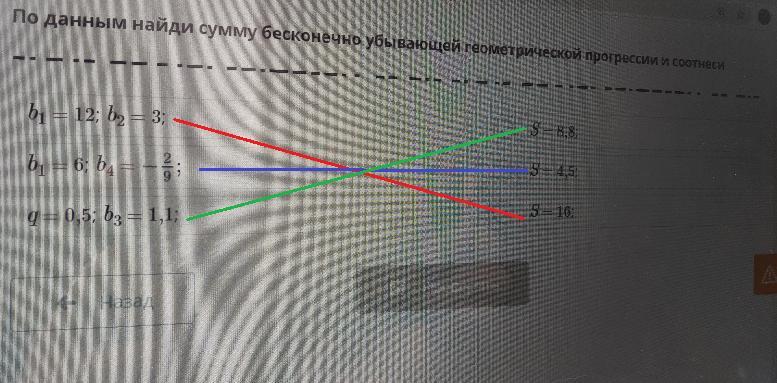
По данным найди сумму бесконечно убывающей геометрической прогрессии и соотнести

Answer 1

Ответ:

Объяснение:

Воспользуемся формулой суммы бесконечной геометрической прогрессии

$S= \dfrac{b{_1}}{1-q} .$

$1) b{_1}= 12, b{_2}= 3;\\q=\dfrac{b{_2}}{b{_1}} ;\\q=\dfrac{3}{12} =\dfrac{1}{4} ;\\S=\dfrac{12}{1-\dfrac{1}{4} } =\dfrac{12}{\dfrac{3}{4} } =\dfrac{12\cdot4}{3} =\dfrac{3\cdot4\cdot4}{3} =16.$

$2) b{_1}=6, b_4}=-\dfrac{2}{9} ;\\\\b{_4}= b{_1} \cdot q^{3} ;\\\\q^{3} = \dfrac{b{_4}}{b{_1} } \\\\q^{3} =\dfrac{-\dfrac{2}{9} }{6} =-\dfrac{2}{9\cdot6} =-\dfrac{1}{27} ;\\\\q=-\dfrac{1}{3} ;\\S= \dfrac{6}{1-\left(-\dfrac{1}{3}\right )} =\dfrac{6}{1+\dfrac{1}{3} } =\dfrac{6}{\dfrac{4}{3} } =\dfrac{6\cdot3}{4} =\dfrac{2\cdot3\cdot3}{2\cdot2} =\dfrac{9}{2} =4,5.$

$3) q=0,5, b{_3}= 1,1;\\\\b{_3}= b{_1}\cdot q^{2} ;$

$b{_1}= \dfrac{b{_3} }{q^{2} };\\\\b{_1}=\dfrac{1,1}{(0,5)^{2} } =\dfrac{1,1}{0,25} =\dfrac{110}{25} = \dfrac{22}{5} =\dfrac{44}{10} =4,4$

$S= \dfrac{4,4}{1-0,5} = \dfrac{4,4}{0,5} =\dfrac{4,4\cdot2}{0,5\cdot2} =\dfrac{8,8}{1} =8,8.$