Найти пределы ( не пользуясь правилом Лопиталя)
На фото(20 вариант 1,2,3 пункт решить надо) очень срочно
Приложения:
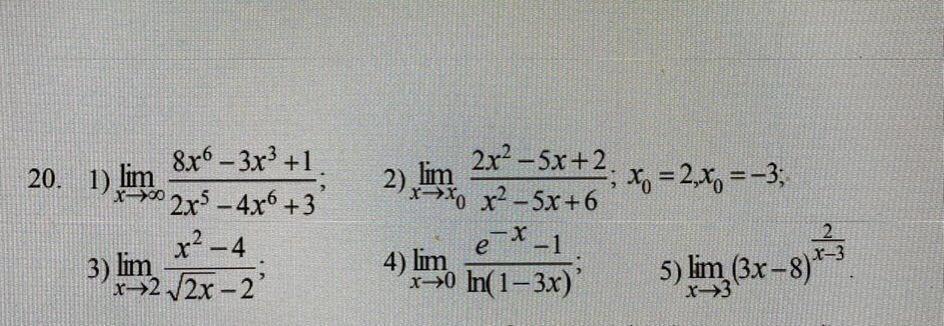
Ответы
Ответ дал:
1
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад