Question

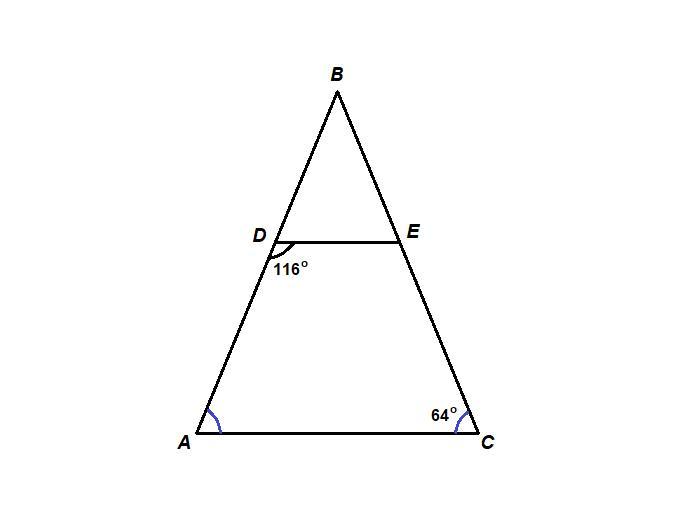
В треугольнике ABC стороны AB = CB. Точки D и E взяты на сторонах AB и CB соответственно. Если ∠ADE = 116°, ∠ACE = 64°, докажи, что прямые DE и AC параллельны.
Заполни пропуски:
Так как по условию задачи AB = CB, то треугольник ABC –
треугольник. По свойству равнобедренного треугольника ∠BAC = ∠BCA =
.
Углы DAC и ADE — это углы
, когда прямые DE и AC пересекаются третьей прямой
. По
признаку параллельности прямых прямые DE и AC параллельны, так как ∠DAC +
= 64° + 116° = 180°.


помогите пожалуйста
дам 40 баллов за правильный ответ!!!​

Answer 1

Ответ:

Так как по условию задачи AB = CB, то треугольник ABC – равнобедренный треугольник.

По свойству равнобедренного треугольника ∠BAC = ∠BCA = 64°.

Углы DAC и ADE — это углы внутренние односторонние, которые образуются, когда прямые DE и AC пересекаются третьей прямой АВ. По третьему признаку параллельности прямых прямые DE и AC параллельны, так как

∠DAC + ∠ADE = 64° + 116° = 180°.