Длины диагоналей трёх граней прямоугольного параллелепипеда, имеющие общую вершину, равны 2 корней из десяти см, 2 корней из семнадцати см и 10 см. Найдите диагональ параллелепипеда.
Ответы
Ответ дал:
0
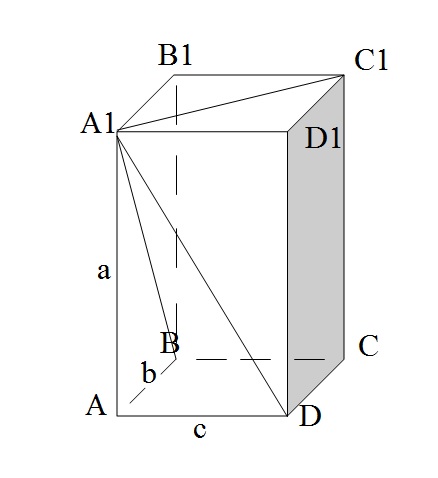
Дан прямоугольный параллелепипед ABCDA1B1C1D1.
А1С1= , А1В=
, А1В= , A1D=10.
, A1D=10.
Обозначим измерения параллелепипеда буквами a, b, c:
АА1=а, АВ=b, AD=с.
Рассмотрим прямоугольные треугольники А1В1С1, А1АВ и А1АD.
По теореме Пифагора:



Выразим a, b и с из этих выражений.











Диагональ параллелепипеда находится по формуле:



А1С1=
Обозначим измерения параллелепипеда буквами a, b, c:
АА1=а, АВ=b, AD=с.
Рассмотрим прямоугольные треугольники А1В1С1, А1АВ и А1АD.
По теореме Пифагора:
Выразим a, b и с из этих выражений.
Диагональ параллелепипеда находится по формуле:
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
11 лет назад