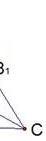Ответы
Объяснение:
Теорема:
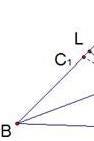
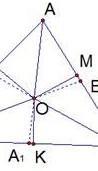
Биссектрисы АА1, ВВ1, СС1 треугольника пересекаются в одной точке О
Доказательство:
Рассмотрим сначала две биссектрисы ВВ1 и СС1. Они пересекаются, точка пересечения О существует. Чтобы доказать это, предположим противное: пусть данные биссектрисы не пересекаются, в таком случае они параллельны. Тогда прямая ВС является секущей и сумма углов <B/2+С/2=180 , это противоречит тому, что во всем треугольнике сумма углов .
Итак, точка О пересечения двух биссектрис существует. Рассмотрим ее свойства:
Точка О лежит на биссектрисе угла B, значит, она равноудалена от его сторон ВА и ВС. Если ОК – перпендикуляр к ВС, OL – перпендикуляр к ВА, то длины этих перпендикуляров равны –OK=OL . Также точка О лежит на биссектрисе УГЛА C и равноудалена от его сторон CВ и СА, перпендикуляры ОМ и ОК равны.
OK=OL
OK=OM
Нас интересует равенство перпендикуляров OL и ОМ. Это равенство говорит о том, что точка О равноудалена от сторон угла A, отсюда следует, что она лежит на его биссектрисе АА1.
Таким образом, мы доказали, что все три биссектрисы треугольника пересекаются в одной точке.
Кроме того, треугольник состоит из трех отрезков, значит, нам следует рассмотреть свойства отдельного отрезка.
Задан отрезок АВ. У любого отрезка есть середина, и через нее можно провести перпендикуляр – обозначим его за р. Таким образом, р – серединный перпендикуляр.
Любая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка.