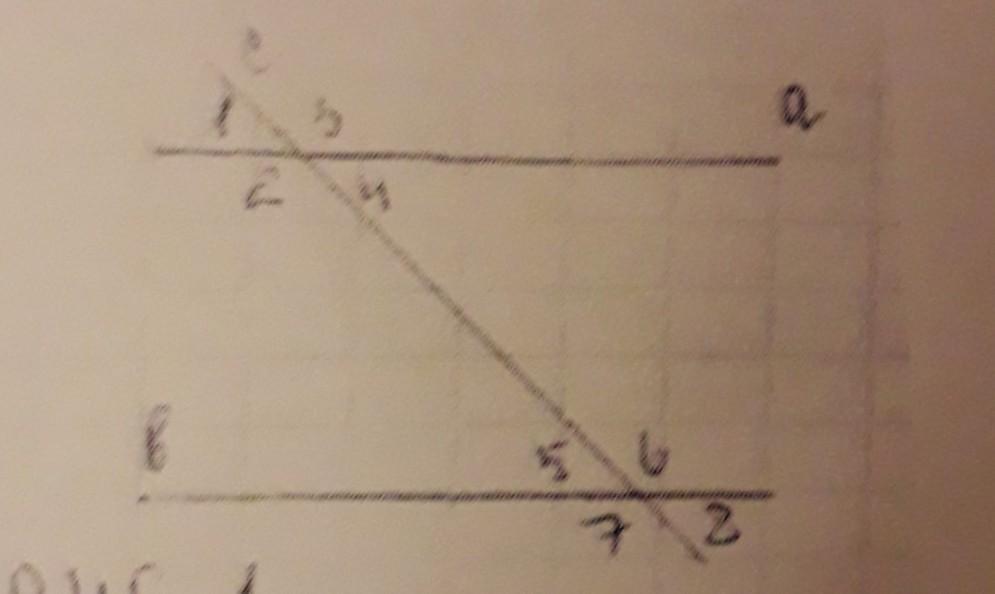Question

1)на рисунке 1 прямые a и b пересечены прямой c.докажите ,что a||b ,если
<1=<8

​

Answer 1

Нужно знать:

1. Виды углов при пересечении двух прямых секущей (см. рис.):

• смежные: ∠1 и ∠3, ∠1 и ∠2, ∠2 и ∠4, ∠3 и ∠4, ∠5 и ∠6, ∠5 и ∠7, ∠6 и ∠8, ∠7 и ∠8;
• вертикальные: ∠1 и ∠4, ∠2 и ∠3, ∠5 и ∠8, ∠6 и ∠7;
• соответственные: ∠1 и ∠5, ∠2 и ∠7, ∠3 и ∠6, ∠4 и ∠8;
• внутренние односторонние: ∠2 и ∠5, ∠4 и ∠6;
• внутренние накрест лежащие: ∠4 и ∠5, ∠2 и ∠6.

2. Признаки параллельности прямых: если при пересечении двух прямых секущей накрест лежащие углы равны или соответственные углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.

3. Свойство смежных углов: сумма смежных углов равна 180°.

4. Свойство вертикальных углов: вертикальные углы равны.

Поэтому:

По условию при пересечении прямых а и b секущей с ∠1 = ∠8. Из рисунка видно, что:

∠1 = ∠4, ∠5 = ∠8 как вертикальные углы, значит, ∠4 = ∠5.

Имеем: ∠4 = ∠5. А т. к. ∠4 и ∠5 - внутренние накрест лежащие углы, то по признаку параллельности прямых прямые а и b параллельны,

т.е. а ║b. Доказано.