Найти площадь фигуры (через определенный интеграл), ограниченной линиями:




Simba2017:
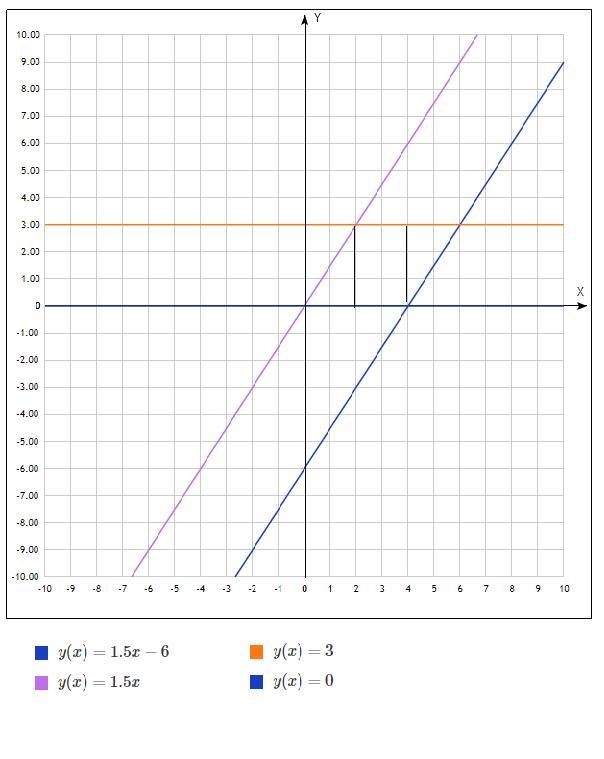
по х от 0 до 2, от 2 до 4, от 4 до 6
функции -уравнения прямых
в чем проблема то?
расписать?
Да, пожалуйста. Для меня эта тема новая, поэтому туплю сильно.
точки пересечения тоже?
или сами их знаете как находить?
Точки пересечения с осью Ох? Знаю.
нет, между самими прямыми, это x=2;4;6
спросите что неясно, а то я ухожу
Ответы
Ответ дал:
1
s=∫1.5x*dx+∫3dx+∫(3-(1.5x-6))dx=+3x+9x-1.5x^2/2=3+6+3=12
a)∫1.5x*dx=1.5x^2/2=1.5*4/2=3
по х от 0 до 2
b)∫3dx=3x=3*4-3*2=6
по х от 2 до 4
с)∫(3-(1.5x-6))dx=∫(9-1.5x)dx=9x-1.5x^2/2=9*6-1.5*36/2-(9*4-1.5*16/2)=
=54-27-36+12=66-63=3
по х от 4 до 6
Приложения:
Всё, я понял. Спасибо большое
а в третьем поняли почему разность?
Потому что функция y = 3 на отрезке [4; 6] больше y = 1.5x-6, поэтому площадь того треугольничка находится через интеграл разности этих функций?
отлично, на предыдущих интервалах так же, просто там внизу прямая у=0 ничего не меняет в разности!
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад