Ответы
Ответ дал:
1
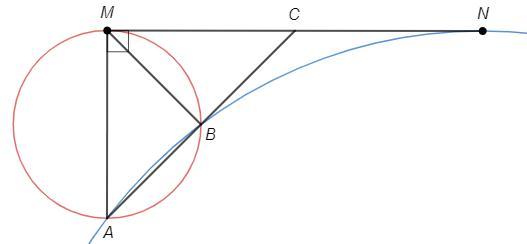
Пусть AB и MN пересекаются в точке С
По теореме о касательной и секущей из одной точки (произведение секущей на её внешнюю часть равно квадрату касательной)
CM^2 =CA*CB
CN^2 =CA*CB
=> CM=CN
(Доказали, что радикальная ось делит пополам отрезки общих касательных между точками касания.)
Тогда AM =MN/2 =CM, ∠AMN=90 =>
△AMN - равнобедренный прямоугольный, ∠MAB=45
∠NMB =∪MB/2 (угол между касательной и хордой равен половине дуги, стягиваемой хордой)
∠MAB =∪MB/2 (вписанный угол)
∠NMB =∠MAB =45°
Приложения:
djdssvjkjd:
MNB=MAB почему?
понятно?
"угол между касательной и хордой равен половине дуги стягиваемой хордой" как можно доказать эту лемму?
или как называется?
??
пусть MA - диаметр (так и есть, потому что радиус в точку касания перпендикулярен касательной). Тогда угол MBA=90, так как опирается на диаметр. CMB=90-AMB=MAB
спасибо большое
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад
