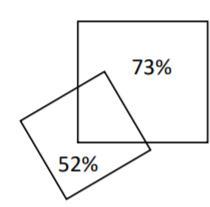
Два квадрата расположены так, как показано на рисунке, при этом у маленького квадрата без их общей части осталось 52% площади, а у большого без их общей части осталось73% площади. Найдите, чему равно отношение сторон квадрата.
Приложения:
Ответы
Ответ дал:
13
Ответ:
48% площади одного = 27% площади другого, т.е.
площадь большего / площадь меньшего = 48/27 = 16/9. Так как площадь пропорциональна квадрату стороны, то стороны этих квадратов будут
соотноситься как корень квадратный из данной дроби, то есть 4/3
Lanaloud:
Помогите? Два квадрата расположены так, как показано на рисунке. Если отсечь от маленького квадрата часть, пересекающуюся с большим, останется 50%50% его площади, у большого без их общей части останется 68%68% площади. Найдите, чему равно отношение стороны маленького квадрата к стороне большого.
50% площади малого = 32% площади большого, пл. большого/пл. малого = 32/50 = 16/25 = х^2 / y^2, x/y = (16/25)^0,5 = 4/5
4/5 - отношение стороны малого квадрата к большому
Вернее так: площадь малого/площадь большого = 32/50 = 16/25 = х^2/y^2, значит соотношение сторон равно х/у = корень из 16/25 = 4/5
у меня вместо 73 стоит 88 помогит
правильный ответ 3/5
100-88=12, значит 12% площади большого равно 48% площади малого, 48/12 = 4 - отношение площадей, √4=2 - отношение сторон, значит сторона большего квадрата в 2 раза больше стороны меньшего
3/5 - в какой задаче это правильный ответ?
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад