Ответы
Ответ дал:
1
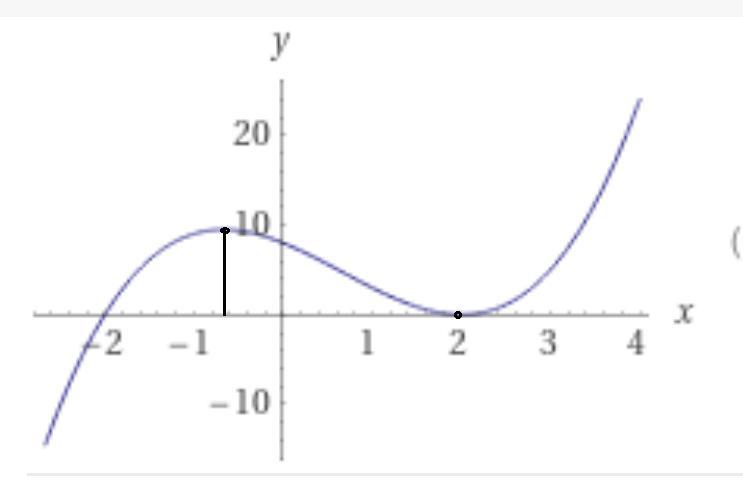
Будем считать, что функция задана так: f(x)=((x-2)^2)×(x+2).
Раскроем скобки: y = x³ - 2x² - 4x + 8.
Производная функции равна: y' = 3x² - 4x - 4.
Приравниваем её нулю: 3x² - 4x - 4 = 0. D = 16+4*3*4 = 64.
x1 = (4-8)/6 = -4/6 = -2/3,
x2 = (4+8)/6 = 12/6 = 2.
Функция возрастает (-∞; (-2/3)) и (2; +∞).
Убывает ((-2/3); 2).
Экстремумы: максимум у = 257/27 при х = (-2/3),
минимум у = 0 при х = 2.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад