Ответы
Ответ:
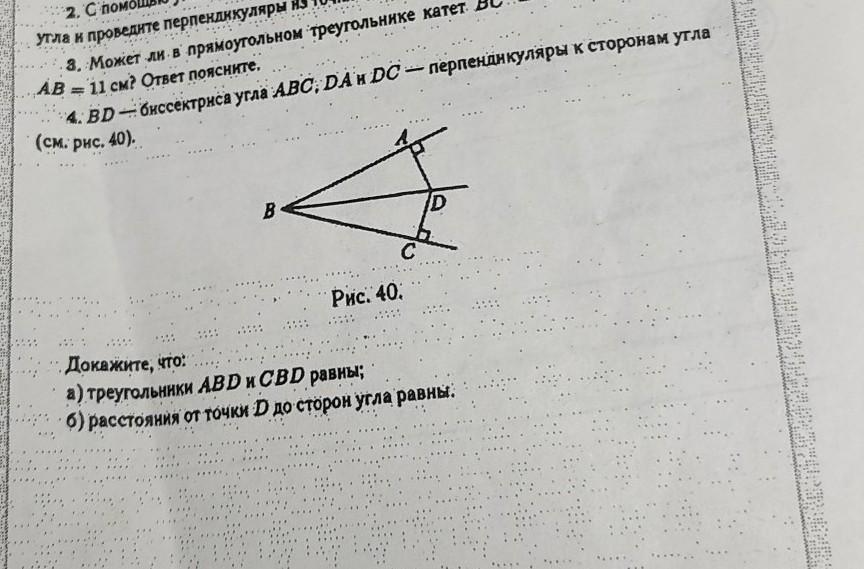
ΔАВС , DA⊥AB , DC⊥BC ⇒ ΔABD и ΔCBD - прямоугольные .
∠ABD=∠CBD , так как BD - биссектриса .
BD является общей стороной (гипотенузой) для указанных треугольников .
ΔABD=ΔCBD по острому углу и гипотенузе (признак равенства прямоугольных треугольников) .
И так как против равных углов лежат равные стороны, то AD=CD .
А это значит, что расстояния от точки D до сторон угла равны (расстояние от точки до прямой измеряется длиной перпендикуляра , проведённого от точки до этой прямой) .
Отсюда вывод: точки, находящиеся на биссектрисе угла равноудалены от сторон этого угла .
Доказательство и пошаговое объяснение:
а) BD - общая сторона
∠DBC = ∠DBA т.к. BD - биссектриса
∠BDC = ∠BDA т.к. ∠А = ∠С = 90, а ∠DBC = ∠DBA.
Тогда по стороне и 2м прилежащим к ней углам ΔABD = ΔCBD
б) Из прошлого доказательства равенства треугольников следует, что соответственные элементы треугольников равны. Расстояние от точки до прямой это перпендикуляр. Значит расстояния до сторон угла равны AD и CD соответственно, а т.к. уже доказано, что ΔABD = ΔCBD, то AD = CD как соответственные элементы. ЧТД