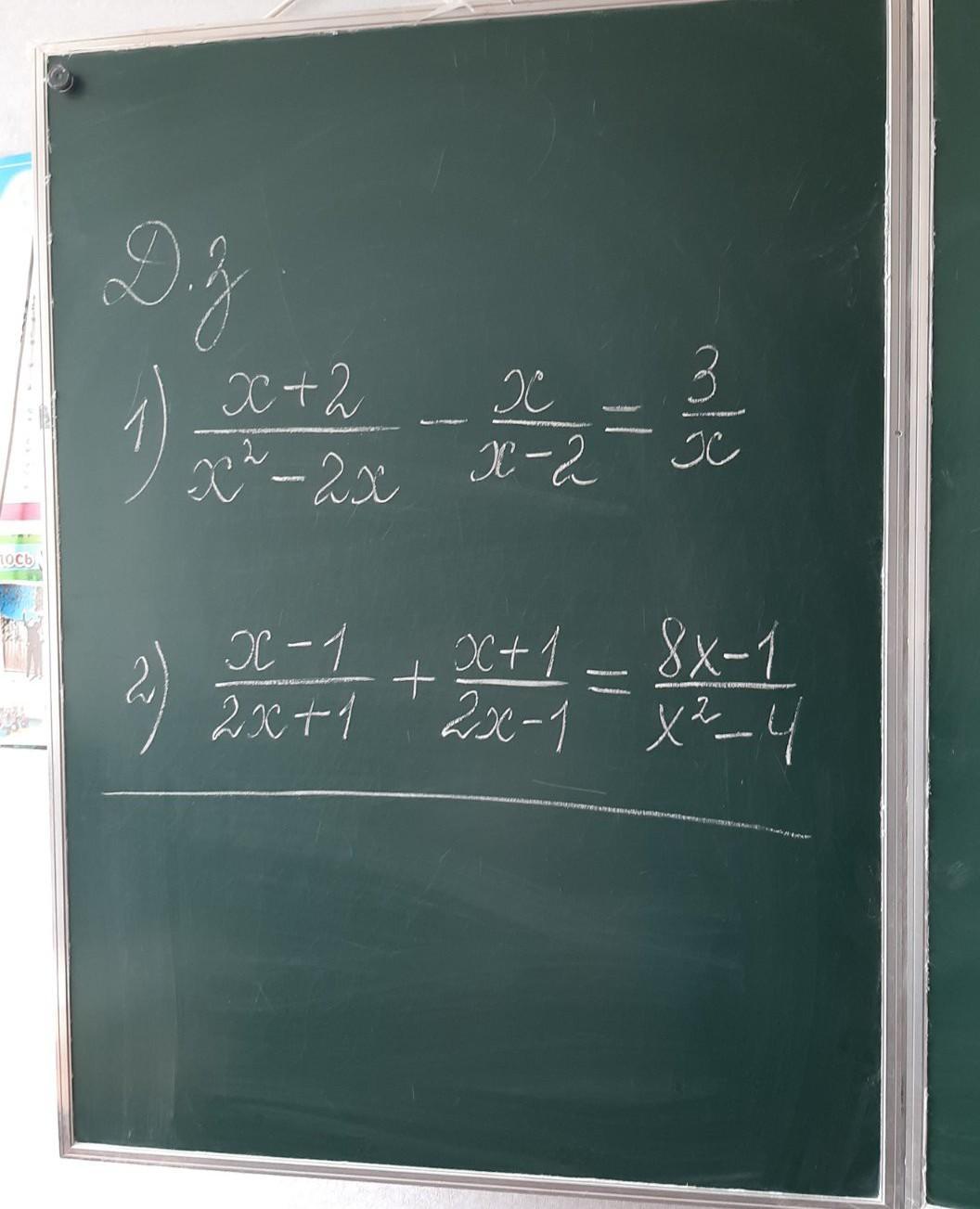Ответы
Ответ дал:
1
Во втором уравнении что то не так в условии
vtsmnnk123:
а там что?
подожди, а че это за красный текст?
С телефона смотрите ?
да, с компа зайти!
??
Да
ок
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад