Question

вычислите интеграл вычислите интеграл

Answer 1

Ответ:

$\int\limits^4_3 {\sqrt{x-3} } \, dx =\\\int\limits {\sqrt{x-3} } \, dx \\\int\limits {\sqrt{t} } \, dt\\\int\limits {t^{\frac{1}{2} } } \, dt\\\frac{2t\sqrt{t} }{3} \\\frac{2(x-3)\sqrt{x-3} }{3} \\\frac{2(x-3)\sqrt{x-3} }{3} ^4_3 \\\frac{2(4-3)\sqrt{4-3} }{3} - \frac{2(3-3)\sqrt{3-3} }{3} \\\frac{2}{3}$

Объяснение:

ответ В

Answer 2

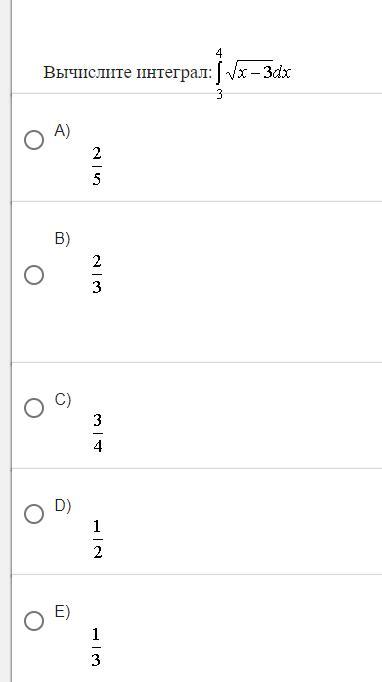
Вычислите интеграл:

$\displaystyle \int\limits_3^4 \sqrt{x - 3} \,dx.$

1. Представим квадратный корень в виде степени с рациональным показателем:

$\displaystyle \int\limits_3^4 (x-3)^{\tfrac{1}{2} } \,dx.$

2. Для функции вида $y = f(kx+b)$ интеграл находится следующим образом:

$\displaystyle \int f(kx + b) \, dx = \frac{1}{k} F(kx + b) + C,$

где $F(kx + b)$ ― одна из первообразных функции $y = f(kx+b),$ $C$ ― произвольная постоянная.

Таким образом, воспользуемся нахождением интеграла степенной функции:

$\displaystyle \int x^{\alpha } = \frac{x^{\alpha + 1}}{\alpha + 1} + C, ~ \alpha \neq -1.$

Имеем:

$\displaystyle \int\limits_3^4 (x-3)^{\tfrac{1}{2} } \,dx = \left\dfrac{(x-3)^{\tfrac{1}{2} +1}}{\dfrac{1}{2} +1} ~ \right|^{4}_{3} = \left\frac{2}{3} \sqrt{(x-3)^{3}} \right|^{4}_{3}$

3. Воспользуемся формулой Ньютона-Лейбница:

$\boxed{\int\limits_a^b f(x)\,dx = F(x) \bigg|^{b}_{a} = F(b) - F(a)}$

Имеем:

$\dfrac{2}{3} \sqrt{(4-3)^{3}} - \dfrac{2}{3} \sqrt{(3-3)^{3}} = \dfrac{2}{3} .$

Ответ: $\dfrac{2}{3}$