Question

Прошу Постройте треугольник по разности двух сторон, углу между ними и стороне, противолежащей этому углу. Задача из темы на осевую симметрию ( может отложениями решится) в подсказке написано рассмотрите симметрию относительно бисскетрисы угла, не помогло. Из Гордина 7-9 кл .

Answer 1

Только потому, что налажал в комментариях.

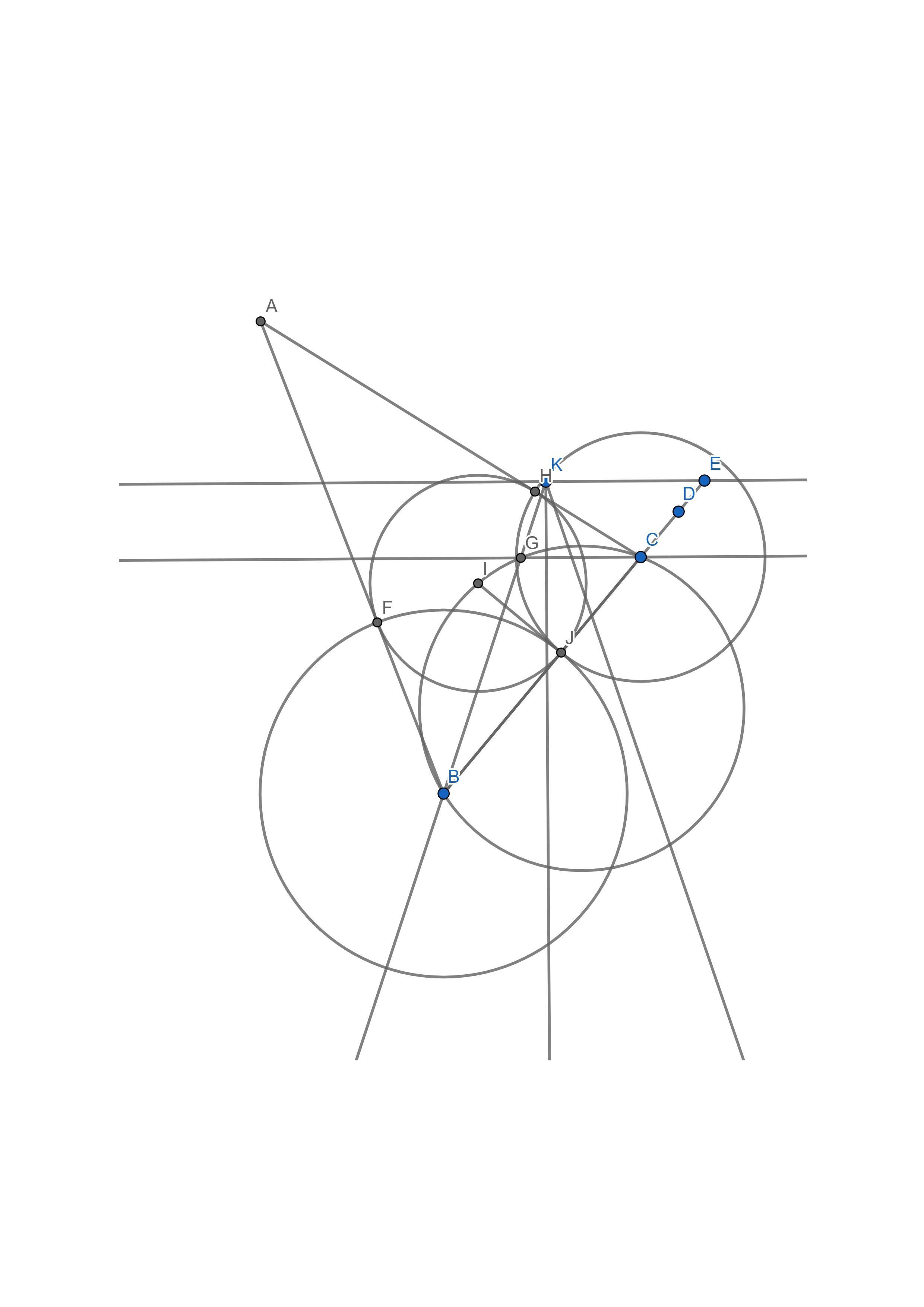
См. чертеж.

1) строится заданный угол φ, на чертеже это угол с вершиной в точке K. Проводится биссектриса и перпендикулярная ей прямая KE. Строится в общем произвольный отрезок BE, концы которого расположены как на чертеже.

Смысл в том, что из точки K отрезок BE виден под углом 90° + φ/2.

2) на отрезке BE от точки B откладывается заданная сторона a, получается точка C. Проводится CG II KE.

Теперь заданная сторона BC = a видна из точки G под углом 90° + φ/2.

3) строится описанная окружность треугольника BCG.

Эта процедура всем известна, я её на чертеже не отображаю, тем более, что GeoGebra строит её автоматически.

4) от точки C во вне отрезка BC откладывается заданная разность d, получается точка D, то есть CD = d. Отрезок BD делится пополам, так находится точка J (то есть BJ = JD).

5) из точки J проводится перпендикуляр к BC до пересечения с окружностью (BGC) в точке I.

I - центр вписанной окружности искомого треугольника

6) проводится окружность с центром I и радиусом IJ.

вписанная окружность.

7) проводятся две окружности - с центром B и радиусом BJ и центром  в C и радиусом CJ. Так находятся точки пересечения этих окружностей с вписанной окружностью  - точки F и H.

Они же - точки касания боковых сторон.

8) проводятся BF и CH до пересечения в точке A.

ABC - искомый треугольник.

Answer 2

Даны угол β, отрезок d=c-a и сторона b.  Исследование. Если на стороне c=AB  нанести точку D такую,   что BD=a, то AD=c-a=d, а угол ADC=90°+B/2 (это следует из того, что треугольник DBC равнобедренный, углы при его основании DC равны  90°-B/2). Эти соображения позволяют провести нужные построения.

Проводим дугу окружности с хордой b=AC, вмещающую угол 90+β/2, и отсекаем на ней хорду   AD=d. Продолжая AD за точку  D до пересечения с дугой окружности, построенной на AC и вмещающей угол  β, находим третью вершину искомого треугольника.