Ответы
Объяснение:
Решение на фото _=______________
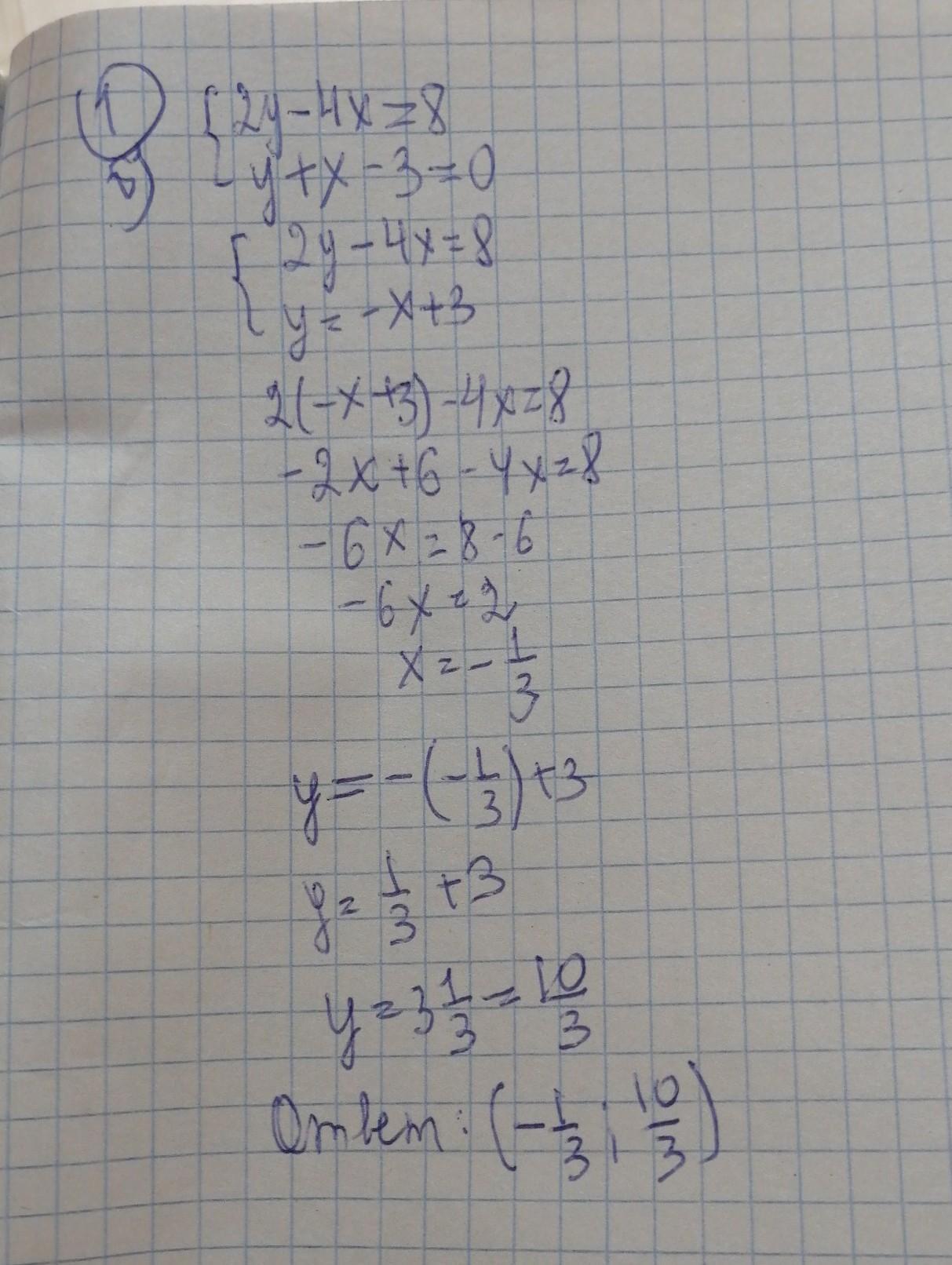
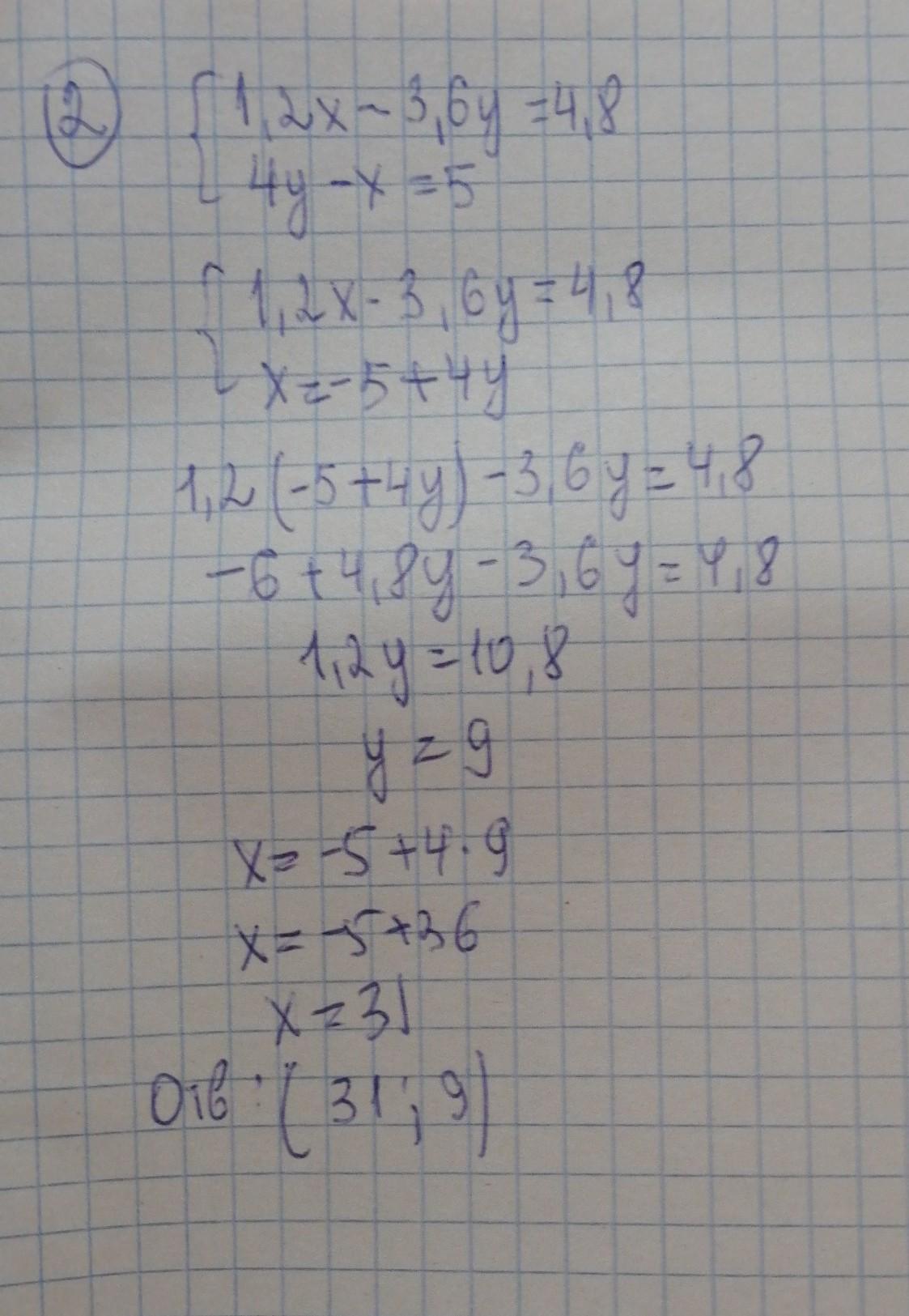
Ответ:
В решении.
Объяснение:
1.
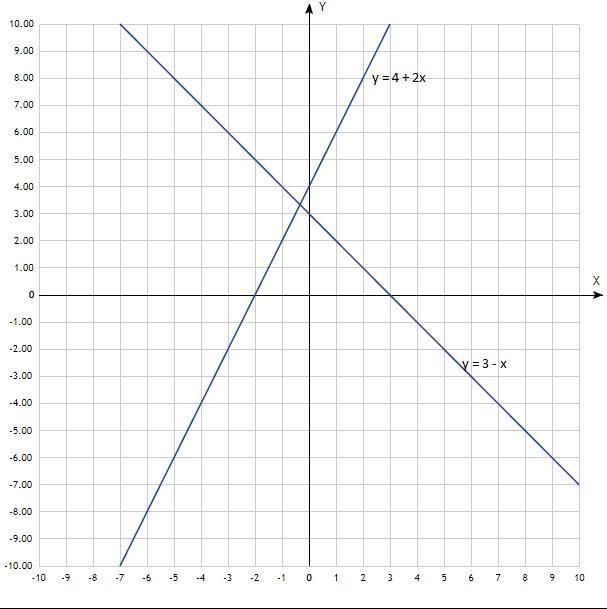
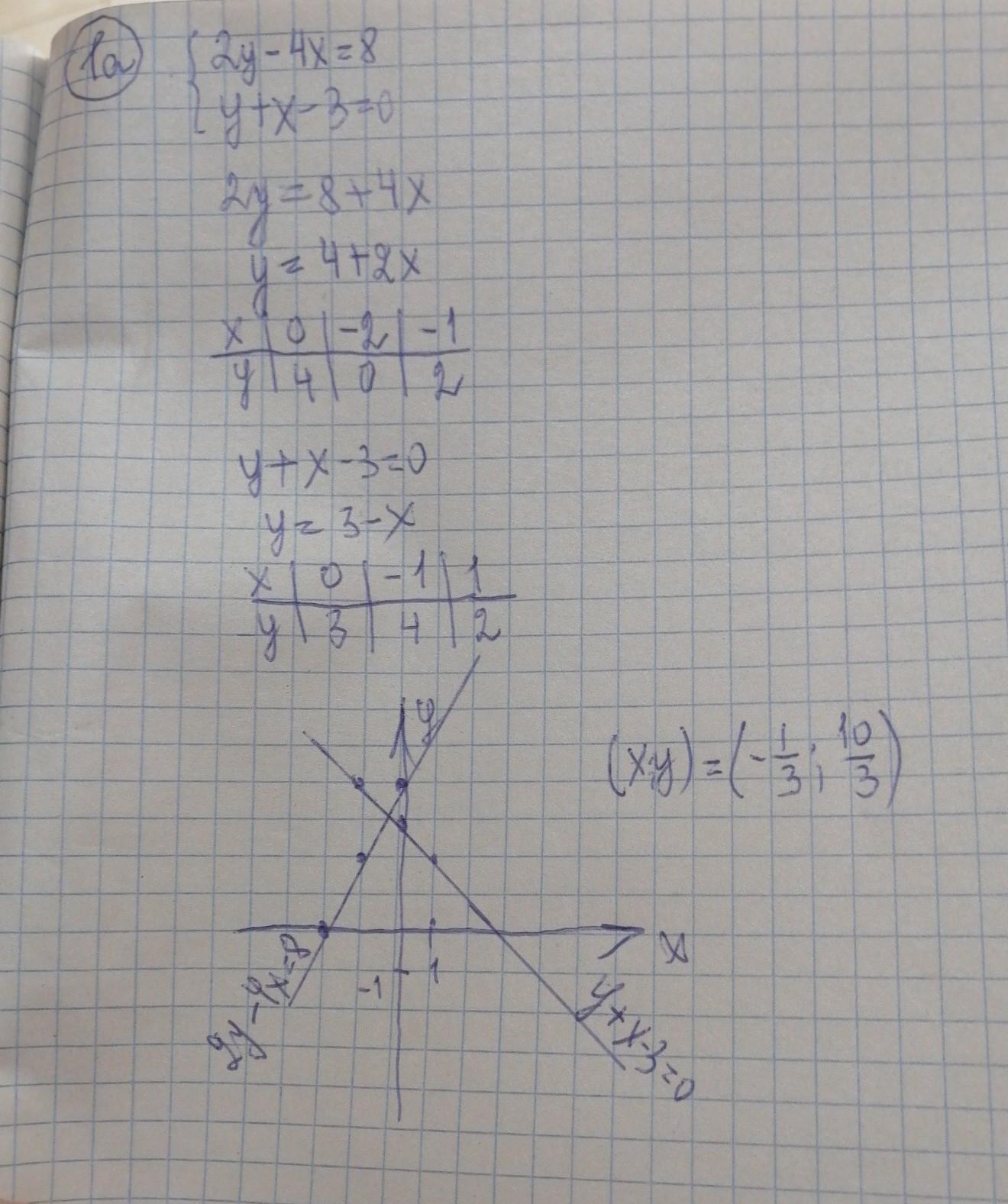
а) Решить систему уравнений графически:
2у - 4х = 8
у + х - 3 = 0
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Прежде преобразовать уравнения в уравнения функций:
2у - 4х = 8 у + х - 3 = 0
2у = 8 + 4х у = 3 - х
у = (8 + 4х)/2
у = 4 + 2х
Таблицы:
х -1 0 1 х -1 0 1
у 2 4 6 у 4 3 2
Координаты точки пересечения прямых (-1/3; 3 и 1/3).
Решение системы уравнений (-1/3; 3 и 1/3).
б) Решить систему уравнений методом подстановки:
2у - 4х = 8
у + х - 3 = 0
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
х = 3 - у
2у - 4(3 - у) = 8
2у - 12 + 4у = 8
6у = 20
у = 20/6
у = 3 и 1/3;
х = 3 - у
х = -1/3.
Решение системы уравнений (-1/3; 3 и 1/3).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
2.
Решить систему уравнений методом подстановки:
1,2х - 3,6у = 4,8
4у - х = 5
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
-х = 5 - 4у
х = 4у - 5
1,2(4у - 5) - 3,6у = 4,8
4,8у - 6 - 3,6у = 4,8
1,2у = 10,8
у = 10,8/1,2
у = 9;
х = 4у - 5
х = 36 - 5
х = 31.
Решение системы уравнений (31; 9).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.