Question

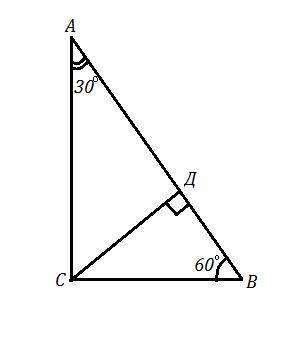
Відрізок – висота прямокутного трикутника , проведена до гіпотенузи. Розв’яжіть трикутник , якщо: а)BD= 4коринь3 ,кутDBC=50°

Answer 1

Відрізок – висота прямокутного трикутника , проведена до гіпотенузи. Розв’яжіть трикутник , якщо: а)BD= 4√3 ,∠тDBC=60°- Уточненные данные .

Т.к DB⊥AC ⇒ ΔDBC-прямоугольный ,∠С=90°-60°=30° ⇒ ВС=2*4√3=8√3 по свойству катета против угла в 30°.

ΔАВС-прямоугольный ,∠А=90°-30°=60° ⇒ АС=8√3*2=16√3 , по свойству катета против угла в 30°.

ΔАВС-прямоугольный , sin60°=AB/AC ⇒ √3/2=AB/16√3 , AB=24.

Ответ. AB=24 , АС=16√3 , ВС=8√3.

Answer 2

Ответ:   АС=24  ,  АВ=16√3  ,  ВС=8√3  .

ΔАВС , ∠С=90°  ,  ∠ДВС=60°  ,  СД⊥АВ  ,  ВД=4√3

Рассм. ΔВДС:  ∠ВДС=90°  ,  ВС=ВД : cos60° = 4√3 : (1/2)= 8√3

∠ВАС=90°-60°=30°

Рассм. ΔАВС:  BC - катет, лежащий против угла ВАС в 30°, равен половине гипотенузы АВ , значит АВ в 2 раза больше  ВС   ⇒  

АВ=2*8√3 = 16√3

 АС  можно найти по теореме Пифагора:

АС²=АВ²-ВС²=16²*3-8²*3=8²*3(4-1)=8²*3*3=8²*3²

АС=√(8²*3²)=8*3=24