На диагонали AC вписанного четырёхугольника ABCD выбраны точки X и Y так, что ∠BXC=∠DYC=∠A. Известно, что AC=18 и AX=5. Найдите длину отрезка XY.

antonovm: 8 ,, решение позже

siestarjoki: i.imgur.com/eZykB1b.png

Ответы

Ответ дал: antonovm

Ответ:

8 ,,,,,,,,,,,,,,,,,,,,,,,,,

Объяснение:

Приложения:

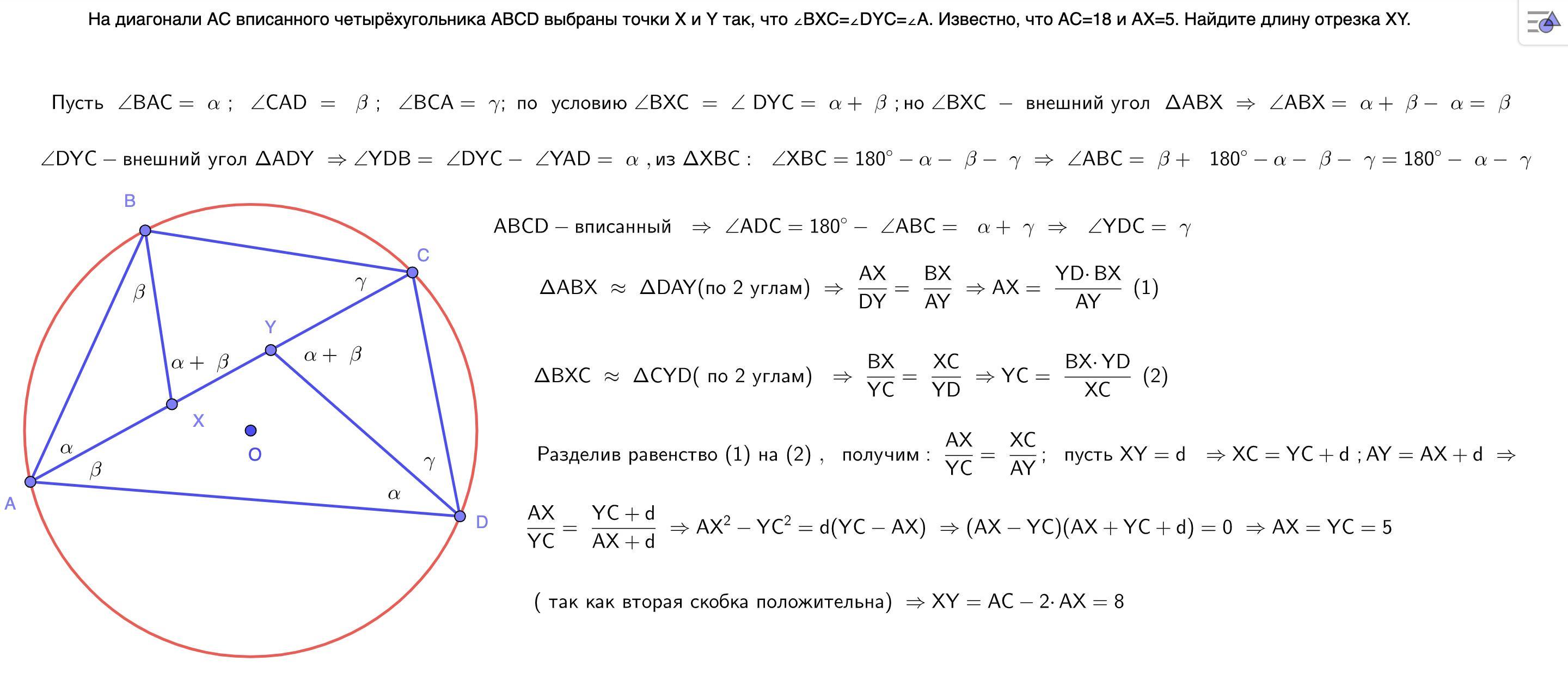
cos20093: У этой задачки есть очень красивый вариант. К нему можно и тут свести. Если диаметр DD₁ пересекает AC в точке H, то X лежит на окружности D₁BH; аналогично BB₁ пересекает AC в F, Y лежит на окружности B₁DF; все это из-за условия на углы. Надо показать, что отрезки хорды AC между исходной окружностью и построенными равны.

cos20093: Доказательство практически такое же дальше - через подобие треугольников. Но благодаря окружностям очень просто доказывать равенство углов.

cos20093: Кстати, и у вас на чертеже - если провести BD, можно сократить доказательство, так как подобны треугольники AXB и BDC => AX = BX*DC/BC;

cos20093: ну а из подобия BXC и DYC CY = BX*DC/BC; :)

Вас заинтересует

Русский язык

1 год назад

Проверочное к слову жесткий з класс

Английский язык

1 год назад

Какая температура у юпитера

Русский язык

2 года назад