Ответы
Ответ дал:
0
Ответ:
х = 1,5
Объяснение:
первая строка - это ОДЗ. в дальнейшем корни будут попадать в допустимую область значений (я уже это формально не проверяла)
поскольку возводили в квадрат, нужна проверка
этот корень не подходит
это наш ответ
ответ
х = 1,5
kotova9797:
эм, я не могу понять откуда 6x взялось, почему у 2x стоит знак минус откуда он взялся??
когда с одной стороны уравнения переменная переносится на другую сторону знак меняется.
так мы ж не переносили не куда 2x почему знак у него поменялся?
и у единицы тоже
Ответ дал:
3
Решение и ответ на фотографии
Приложения:
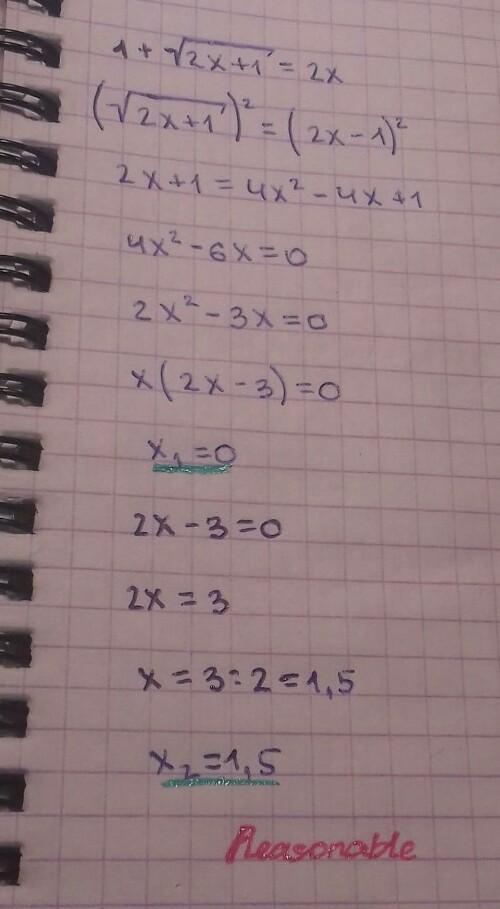
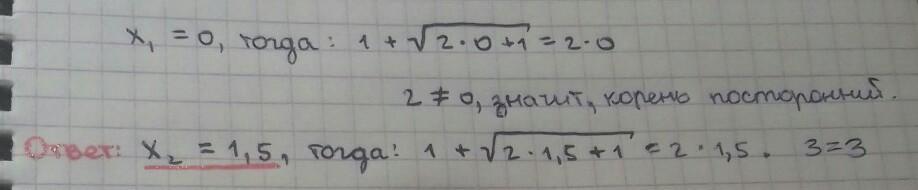
там ведь должно быть 4x^2+4x+1?почему - 4X?
Это квадрат разности, все правильно: (а-b)2= a2-2ab+b2
Вас заинтересует
2 года назад
2 года назад
3 года назад
10 лет назад