Найдите производную функции, но без дифференцирования

Аноним:
Для примера есть производная x^2-2x, получаем 2x-2, это я понимаю как сделать, а как решать вот мою производную? Смотрел в Photomath там используется d/dx
Учитель сказал, что d/dx использовать нельзя
Простите за глупые вопрос, пересдаю математику в колледже
Опишите, как Вы бы решали приведенный пример с x^2-2x
То есть как Вы придёте к указанному ответу
(x^2-2x)' = (x^2)' - (2x)' = (2*x^2-1) - (1*2^1-1) = 2x^1 - 2
где (1*2^1-1) забыл x, должно быть (1*2x^1-1)
Отлично, Вы использовали табличную производную от степенной функции и правило дифференцирования разности функций. Но указанный в задаче случай - не табличная функция, здесь единственный выход для уровня 10 класса - использовать правило производной произведения ( что Вам и указывали ранее: (u*v)'=u'v+uv')
Спасибо Вам большое. Вы мне помогли!
df/dx - это просто одно из обозначений производной функции f по переменной x
Ответы
Ответ дал:
1
Решение задания прилагаю
Приложения:
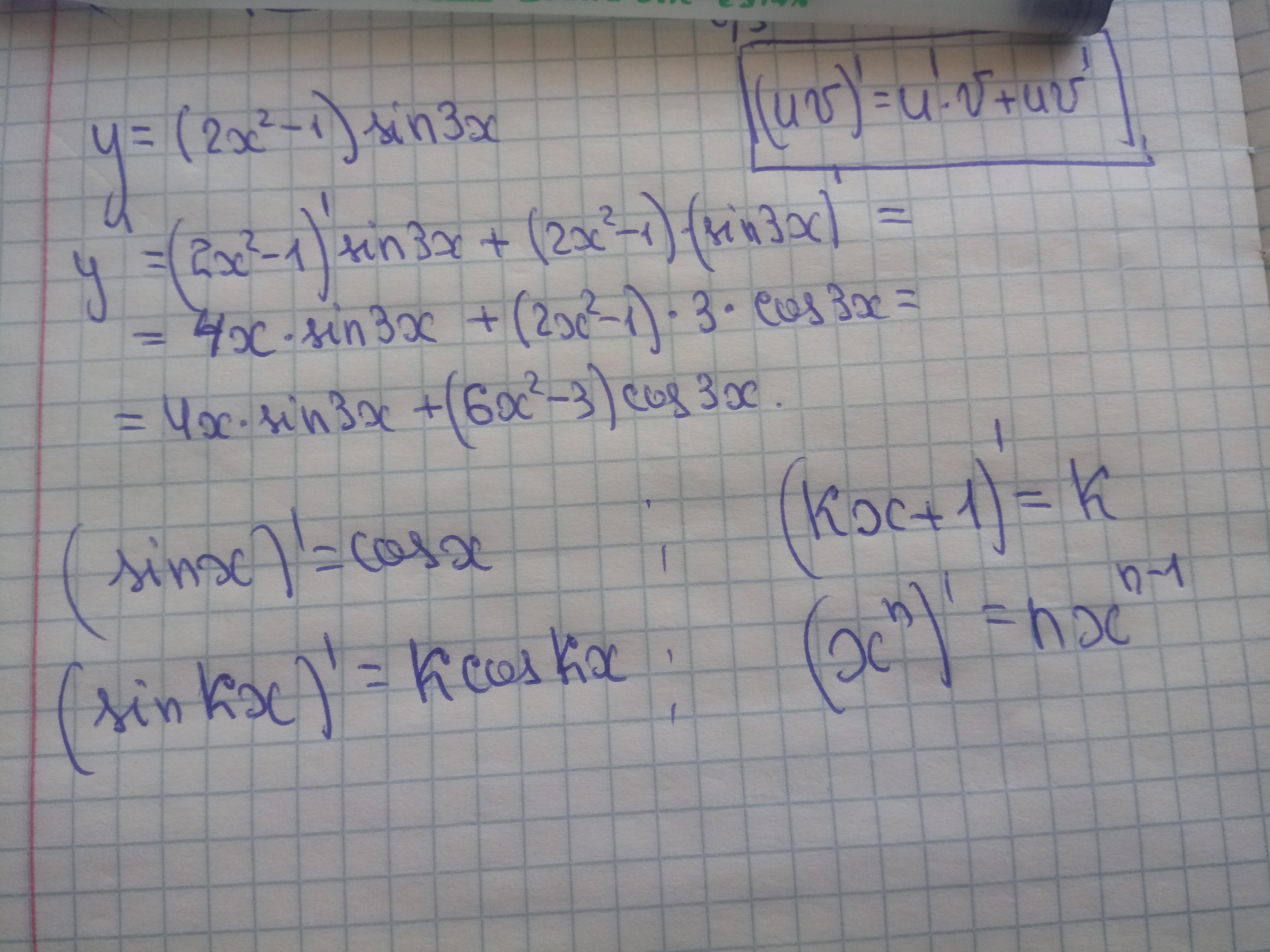
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад