Ответы
Ответ дал:
2
Знаменатель не равен нулю 0,5√5*x-1≠0 и 0,5√5*x-3≠0 ⇒ x≠ ,x≠
обозначим 0,5√5*x-1=a
общий знаменатель а(а-2)
,a²-5a+4=0 ,D=9 , a₁=1 ,a₂=4
,
методинтервалов + + + + +(0) - - - - [1]+ + + + (2)- - - - [4] + + + + +
0<a≤1 , a≥2.
0<0,5√5*x-1≤1 , 2<0,5√5*x-1≤4
1<0,5√5*x≤2 , 3<0,5√5*x-1≤5
,
учтем x≠
⇒
Ответ ( ;
] , (
;
] .
IUV:
подставьте например х=0 (принадлежит ответу) , получите -2+2/3 >= 2 - ложное выражение
точно.гдетоошибся
-2а*(-2) неправильно умножил. Ну как исправить то?
мой косяк - отметил нарушением.
теперь прийдется ждать вмешательства модератора чтобы отправил на исправление
теперь прийдется ждать вмешательства модератора чтобы отправил на исправление
удалят меня
ну ладно
если вложен труд то обычно отправляют на исправление
ПОСЛЕ ИСПРАВЛЕНИЯ - в ответе там где 6 делить на корень из пяти тоже должна быть круглая скобка
да, вы правы
да
Ответ дал:
3
Ответ:
во вложении
Пошаговое объяснение:
Приложения:
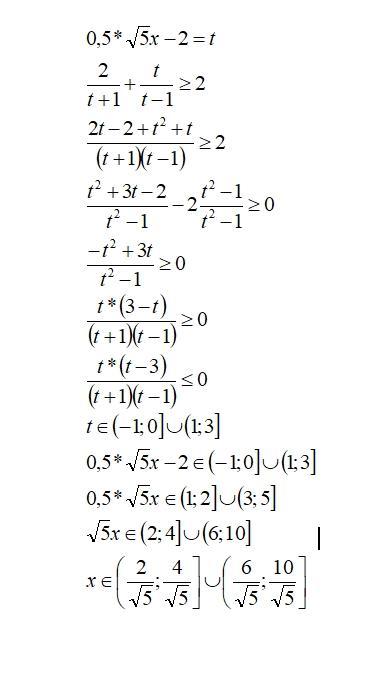
этот верное решение, мискликнул и не тому лучший ответ дал
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад