Доведіть, що коли через дану точку до кола проведено дві дотичні, то відрізки дотичних, які сполучають дану точку з точками дотику, piвнi
Ответы
Ответ дал:
1
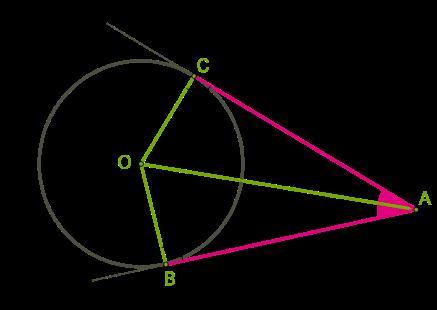
Нехай AB та AC — дотичні до кола з центром O. Потрібно довести, що AB = AC та OA є бісектрисою кута A.
Трикутники OBA та OCA — прямокутні, оскільки дотичні перпендикулярні до радіусів кола у точках B та C. Сторона OA — спільна. Катети OB та OC рівні як радіуси одного й того самого кола. Трикутники рівні за гіпотенузою та катетом, звідси рівні й катети AB та AC, а також кути BAO і CAO, тобто OA ділить кут навпіл.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад