решите способом подстановки систему уравнений :
(через Дискриминант)
Пример 3,6.
Пожалуйста, очень нужно.
Приложения:
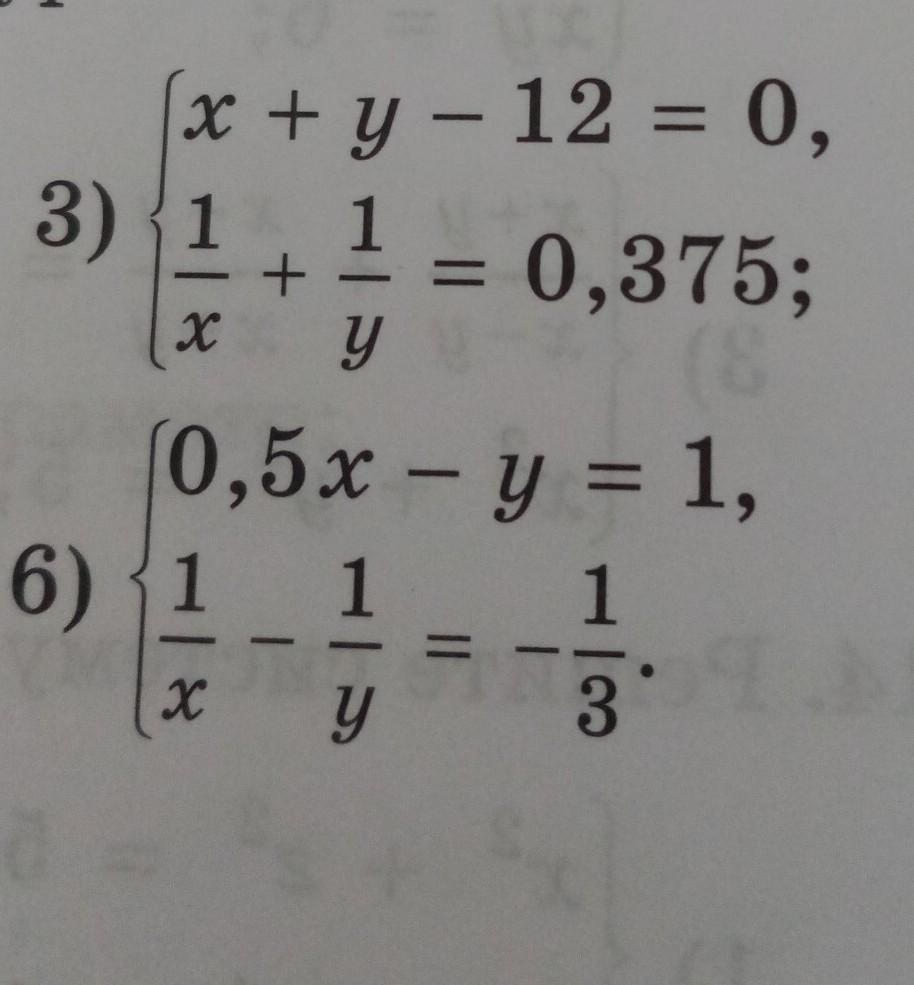
Аноним:
Вот эти две системы уравнений через подстановку?
Ответы
Ответ дал:
0
Ответ:
Объяснение:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад