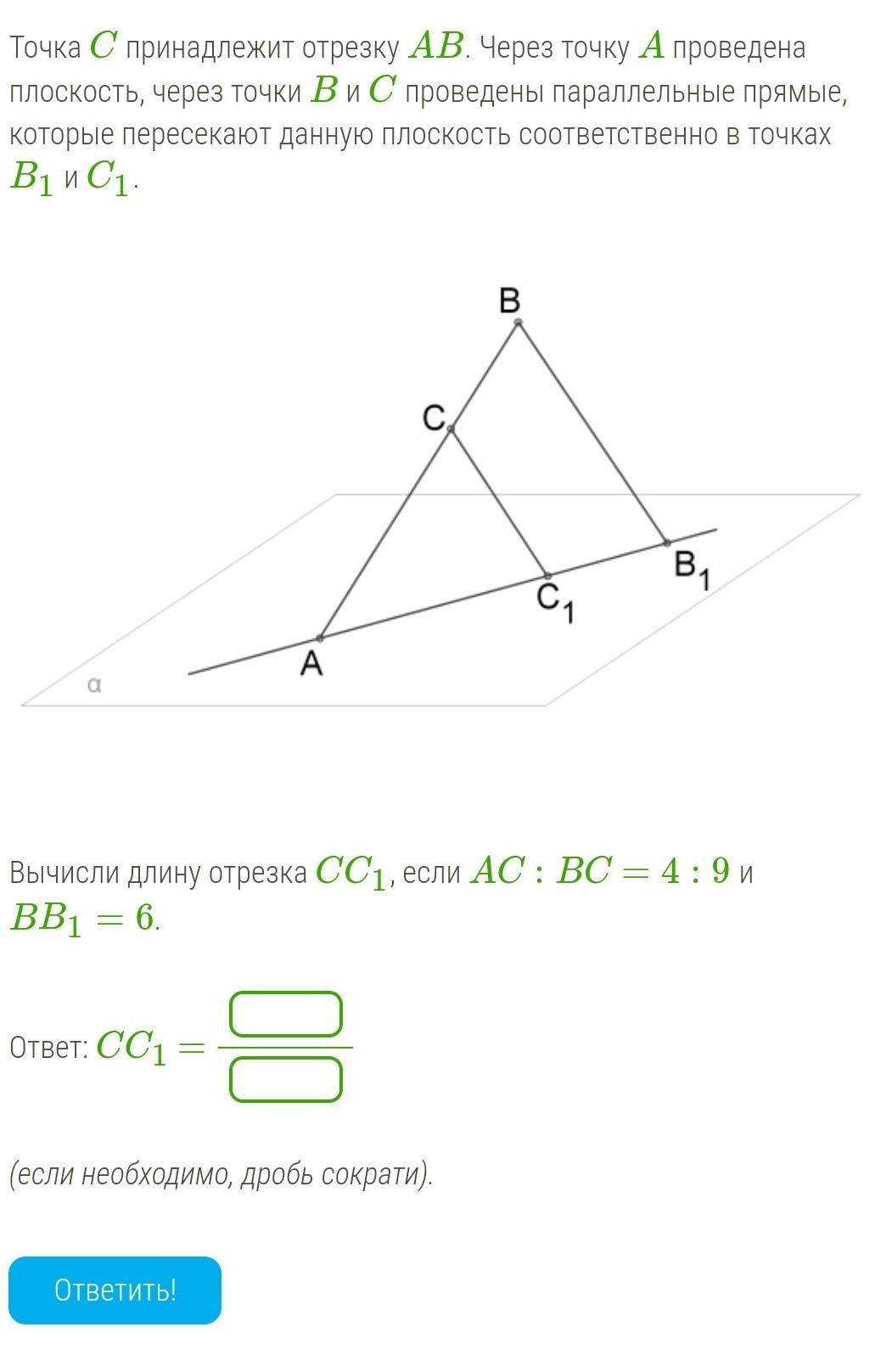
Точка C принадлежит отрезку AB. Через точку A проведена плоскость, через точки B и C проведены параллельные прямые, которые пересекают данную плоскость соответственно в точках B1 и C1.
Вычисли длину отрезка CC1, если AC:BC=4:9 и BB1=6.
Ответ: CC1 =
Приложения:
Ответы
Ответ дал:
4
Ответ:
Объяснение:
Пусть АС = 4х, тогда ВС = 9 х и АВ = 4х + 9х = 13х
Треугольники АВВ₁ и АСС₁ подобны по двум углам: ∠А - общий и ∠В = ∠С - соответственные углы при СС₁ ║ ВВ₁ и секущей АВ.
Из подобия треугольников следует пропорциональность соответствующих сторон:
СС₁ : ВВ₁ = АC : АB
откуда
ruslanfe:
Следовательно, BB1:CC1=AB:AC или CC1=BB1⋅AC:AB=6*4х:13х=24/13
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад