Question

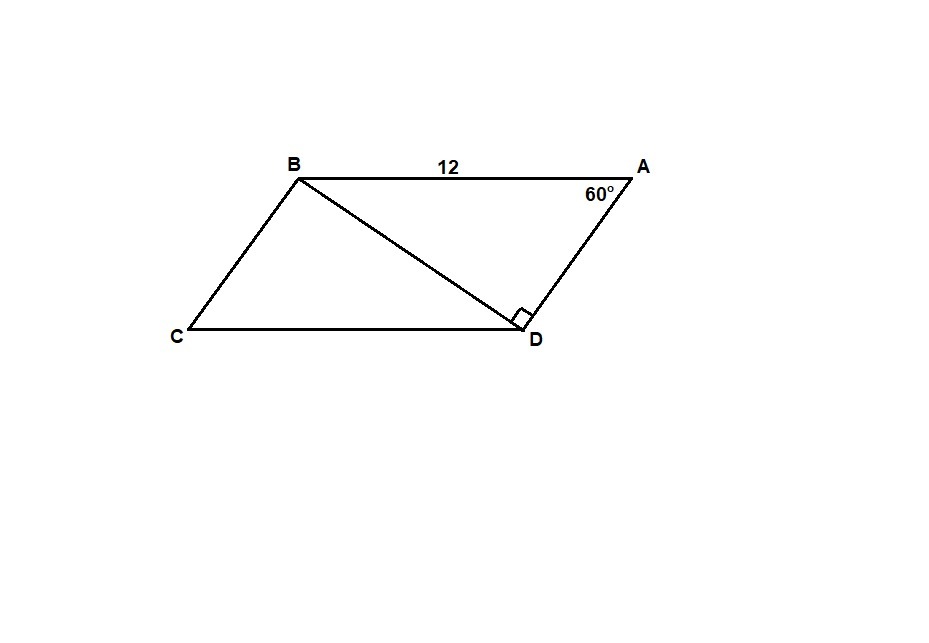
Диагональ BD параллелограмма ABCD перпендикулярна к сторонам AD,AB=12 см,угол А=60°.Найдите площадь паралелограмма ABCD.

ПОМОГИТЕ ПОЖАЛУЙСТА! ПИШИТЕ ЧТО НАДО БУДЕТ-ОТВЕЧУ!

Answer 1

ΔABD: ∠ADB = 90°, ∠BAD = 60°, ⇒ ∠ABD = 30°, напротив угла в 30° лежит катет, равный половине гипотенузы, поэтому

           AD = 1/2 AB = 1/2 · 12 = 6 см

           По теореме Пифагора:

           BD² = AB² - AD² = 12² - 6² = 144 - 36 = 108

           BD = √108 = 6√3 см

BD - высота параллелограмма, проведенная к стороне AD.

Sabcd = AD · BD = 6 · 6√3 = 36√6 см²