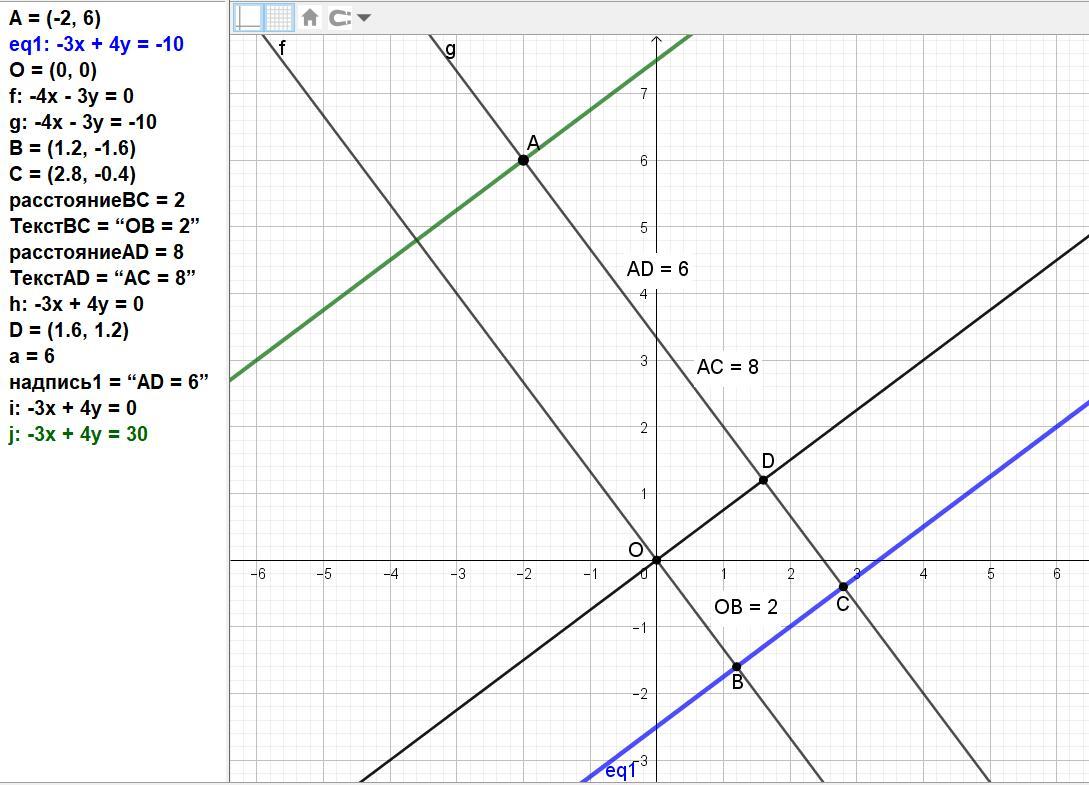
1) Записати рівняння прямої -Зх+4у+10=0 у нормальній
формі. За допомогою одержаного рівняння знайти відстань від точки А(-2;6) до прямої.
2) Написати рівняння кола, що проходить через точки перетину
кола x^2+у^2+4x-4y = 0 з прямою у=-x і через точку А(4;4).
3) Написати рівняння дотичних до кола x^2+у^2-8x-4у+16 = 0
які проведено з початку координат.
Ответы
1) Записати рівняння прямої -Зх+4у+10=0 у нормальній формі. За допомогою одержаного рівняння знайти відстань від точки А(-2;6) до прямої.
Общее уравнение прямой можно привести к нормальному виду. Пусть
Ax + By + C = 0 - общее уравнение прямой, a
xcos α + ysin α – p = 0 - её нормальное уравнение.
Так как оба уравнения определяют одну и ту же прямую, их коэффициенты пропорциональны.
Очевидно, для получения нормального уравнения следует все члены общего уравнения умножить на постоянный множитель μ , вычисляемый по формуле
μ = +- 1/√(A² + B²)
В этой формуле берётся знак, противоположный знаку C в общем уравнении прямой.
Таким образом, получаем уравнение
μAx + μBy + μC = 0
которое и будет нормальным уравнением прямой на плоскости.
Находим значение множителя –μ (так как в уравнении слагаемое С = + 10).
-μ = -1/√((-3)² + 4²) =-1/√(9 + 16) = -1/√25 =-1/5.
Получаем уравнение заданной прямой в нормальном виде:
–(-1/5)*Зх + (-1/5)*4у + (-1/5)*10 = 0,
(3/5)x - (4/5)y - 2 = 0.
Значение свободного члена равно расстоянию от начала координат до прямой. Оно равно 2.
Подставим координаты заданной точки А(-2; 6) в уравнение.
(3/5)*(-2) - (4/5)*6 - 2 = 0.
(-6/5) – 24/5) – 2 = (-30/5) – 2 = -6 - 2 = -8.
Получили расстояние от точки А до прямой, равное 8.
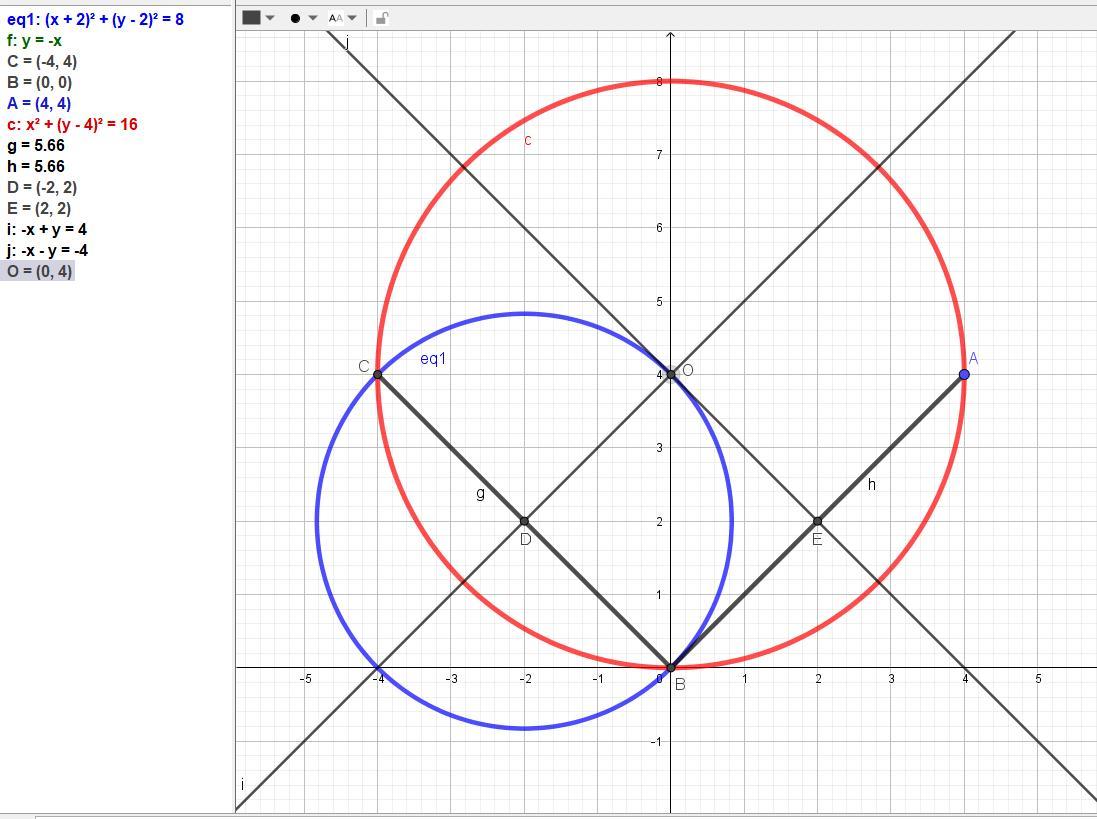
2) Написати рівняння кола, що проходить через точки перетину
кола x^2+у^2+4x-4y = 0 з прямою у=-x і через точку А(4;4).
Для определения точки пересечения надо решить систему:
{x^2+у^2+4x-4y = 0
{у=-x.
Применим способ подстановки.
x^2 + (-x )^2 + 4x – 4*(-x) = 0,
2 x^2 + 8x = 0,
x^2 + 4x = 0,
x(x + 4) = 0.
х1 = 0, х2 = -4,
у1 =0, у2 = 4.
Найдены 2 точки пересечения окружности с прямой:
B(0; 0) и C(-4; 4). Третья точка задана А(4; 4).
Необходимо составить уравнение окружности, проходящей через 3 точки.
Эту задачу можно решить двумя способами:
- а) решить систему из трёх уравнений окружности, в каждом из которых будут координаты одной из точек,
- б) найти центр окружности как точку пересечения перпендикуляров к серединам отрезков, соединяющих точки окружности.
а) Написать уравнение окружности, проходящей через три точки: (4, 4); (0, 0); (-4, 4).
Решение.
Искомое уравнение имеет вид (x - a)2 + (y - b)2 = r2. Поскольку окружность проходит через заданные точки, координаты каждой из этих точек удовлетворяют уравнению окружности. Подставляя поочередно в искомое уравнение координаты данных точек А(4; 4), B(0; 0) и C(-4; 4), получим три уравнения для определения a, b и r. Вот эти уравнения:
{(4 – a)² + (4 – b)² = r²
{(0 – a)² + (0 – b)² = r²
{(-4 – a)² + (4 – b)² = r²
Возьмем уравнения первое и второе, а потом первое и третье. Правые части этих уравнений между собой равны, значит, равны и левые их части, и мы получаем
(4 – a)² + (4 – b)² = {(0 – a)² + (0 – b)²
(4 – a)² + (4 – b)² = (-4 – a)² + (4 – b)²
16 – 8a + a² + 16 – 8b + b² = a² + b²
16 – 8a + a² = 16 + 8a + a²
Раскрывая скобки и упрощая, будем иметь
8a + 8b = 32
16a = 0
Отсюда находим значения a = 0, b = 4.
Подставляя эти значения a и b во второе из уравнений системы, получим
(0 – 0)² + (0 – 4)² = r²
r = 4
Искомое уравнение имеет вид (x – 0)² + (y – 4)² = 4²
или после упрощений получаем каноническое уравнение
x² + (y – 4)² = 4².
Оно же в общем виде x2 + y2 - 8y = 0
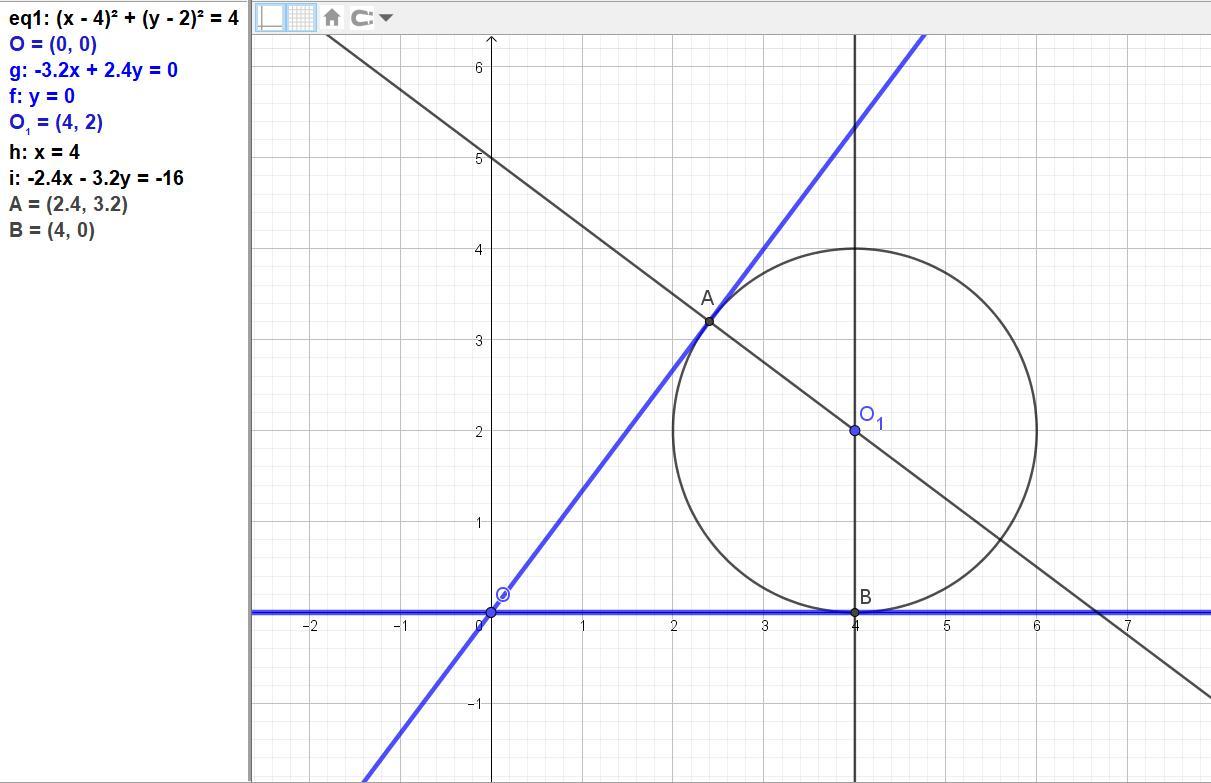
3) Написати рівняння дотичних до кола x² + у² - 8x - 4у + 16 = 0
які проведено з початку координат.
Заданное уравнение приведём к каноническому виду (x – a)² + (y – b)² = r², из которого определим координаты центра и радиус.
(x² - 8x + 16) - 16 + (у² - 4у + 4) – 4 + 16 = 0
(x – 4² + (у – 2)² = 2².
Получили a = 4, b = 2, r = 2.
Так как ордината центра и радиус совпадают, то одна из касательных совпадает с осью Ох. Её уравнение у = 0.
Уравнение второй касательной можно найти с помощью формулы для определения углового коэффициента , или с применением производной, или найти точку касания, а затем по двум точкам составить уравнение.
Применим формулу углового коэффициента касательной:
k = ((x1 – x0)(y1 – y0) + R√((x1 – x0)² + (y1 – y0)² - R²)) / ((x1 – x0)² - R²) =
= ((0 – 4)(0 – 2) + 2√((0 – 4)² + (0 – 2)² - 2²) / (((0 – 4)² - 2²) =
= (8 + 2√16 + 4 – 4) / (16 – 4) = (8 + 2*4)/12 = 16/12 = 4/3.
Получаем уравнение второй касательной:
y = (4/3)(x -4) + 2 = (4/3)x – (16/3) + 2 = (4/3)x – (10/3) или в общем виде
4x – 3y – 10 = 0.