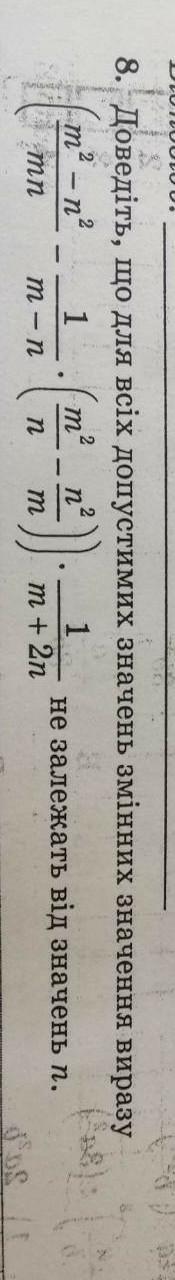Ответы
Ответ дал:
0
Упростим выражение:
Так как в упрощённом выражении нет переменной n, то и его значение не зависит от неё.
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад