Question

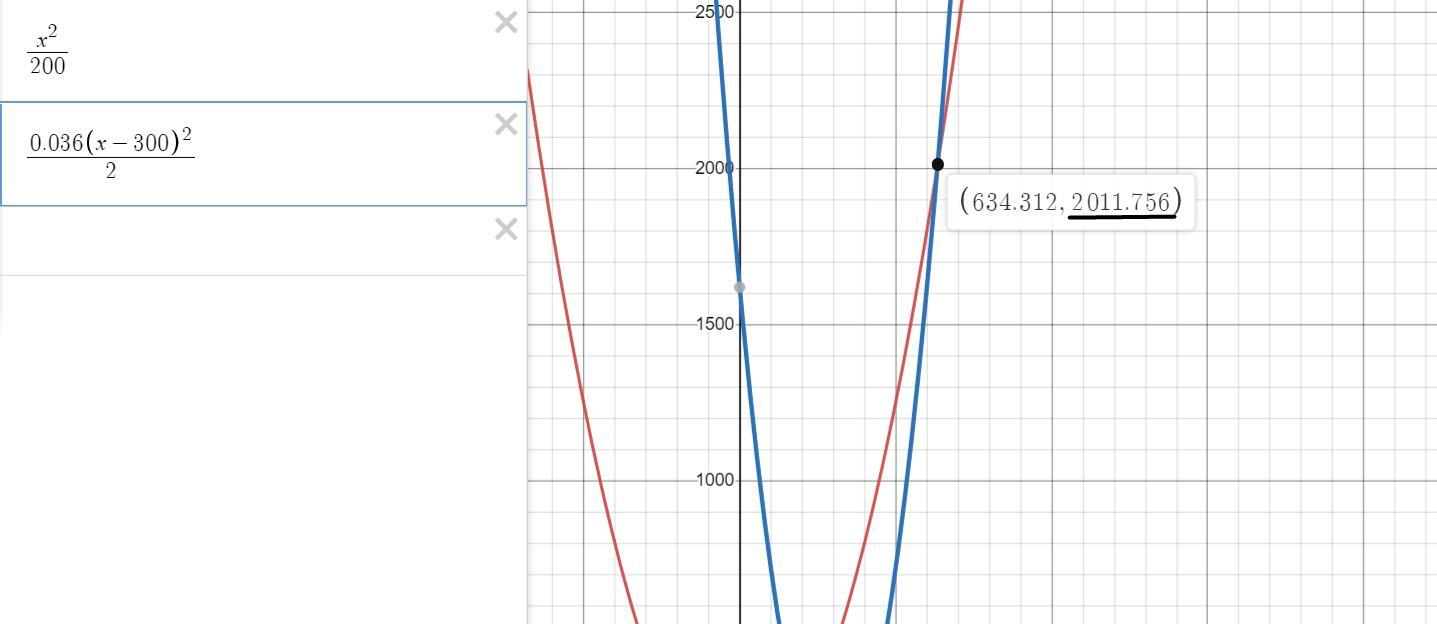
Неудачливый покупатель отъехал от магазина на велосипеде ровно в 10:00, однако забыл свои покупки на кассе. Камеры слежения фиксировали его скорость в течение некоторого времени (см. рисунок).



Прошло 5 минут и от того же магазина в том же направлении отъехал администратор на электросамокате с его покупками.

Определите, какое ускорение должно быть у электросамоката, чтобы догнать покупателя на расстоянии 2 км от магазина. Движение в задаче считать равноускоренным. Ответ представить в м/с2 и округлить до тысячных.

Answer 1

Дано:

График

l = 2 · 10³ м

Δt = 300 c

v - ?

Запишем уравнение скорости при равноускоренном движении:

$v(t) = v_0 + at$

Поскольку график проходит через точку (0;0), можно сказать, что v₀ = 0 м/с, и уравнение перепишется следующим образом:

$v(t) = at$

Если взять координату магазина за 0, чтобы упростить расчеты, то мы можем записать формулу расстояния, которое преодолевает тело с равноускоренным движением:

$l = \dfrac{at^2}{2}$

Исходя из этого, можно найти время, которое проедет покупатель до встречи с администратором.

$t = \sqrt{\dfrac{2l}{a}}$

Поскольку время движения администратора было на 5 минут меньше, то

$\tau = t - 300$, где τ - время движения администратора.

Используем уже записанную формулу для расстояния, пройденного тела при равноускоренном движении:

$l = \dfrac{a_1\tau^2}{2} \longrightarrow a_1 = \dfrac{2l}{\tau^2}$

Запишем конечную формулу, используя тот факт, что a = v(t₀) ÷ t₀, где t₀ - определенное время, прошедшее с 10:00, в секундах.

Имеем:

$a_1 = \dfrac{2l}{\tau^2} = \dfrac{2l}{(t-300)^2} = \boxed{ \dfrac{2l}{(\sqrt{\dfrac{2l*t_0}{v(t_0)}}-300)^2}} }$

Возьмем для удобство точку 10:05 (то есть 300 секунд после начала движения) на графике. Ей соответствует 3 м/с.

Подставим эти значения, а также значение l.

$a_1 = \dfrac{2l}{\tau^2} = \dfrac{2l}{(\sqrt{\dfrac{2l*t_0}{v(t_0)}}-300)^2}} = \dfrac{2*2*10^3}{(\sqrt{\dfrac{2*2*10^3*300}{3}}-300)^2}} = \dfrac{4000}{(\sqrt{40000}-300)^2}} =\dfrac{4000}{(200\sqrt{10}-300)^2}}=\dfrac{4000}{100^2(2\sqrt{10}-3)^2}} = \dfrac{0.4}{49 - 12\sqrt{10}} \approx 0.036$[a] = м/с²

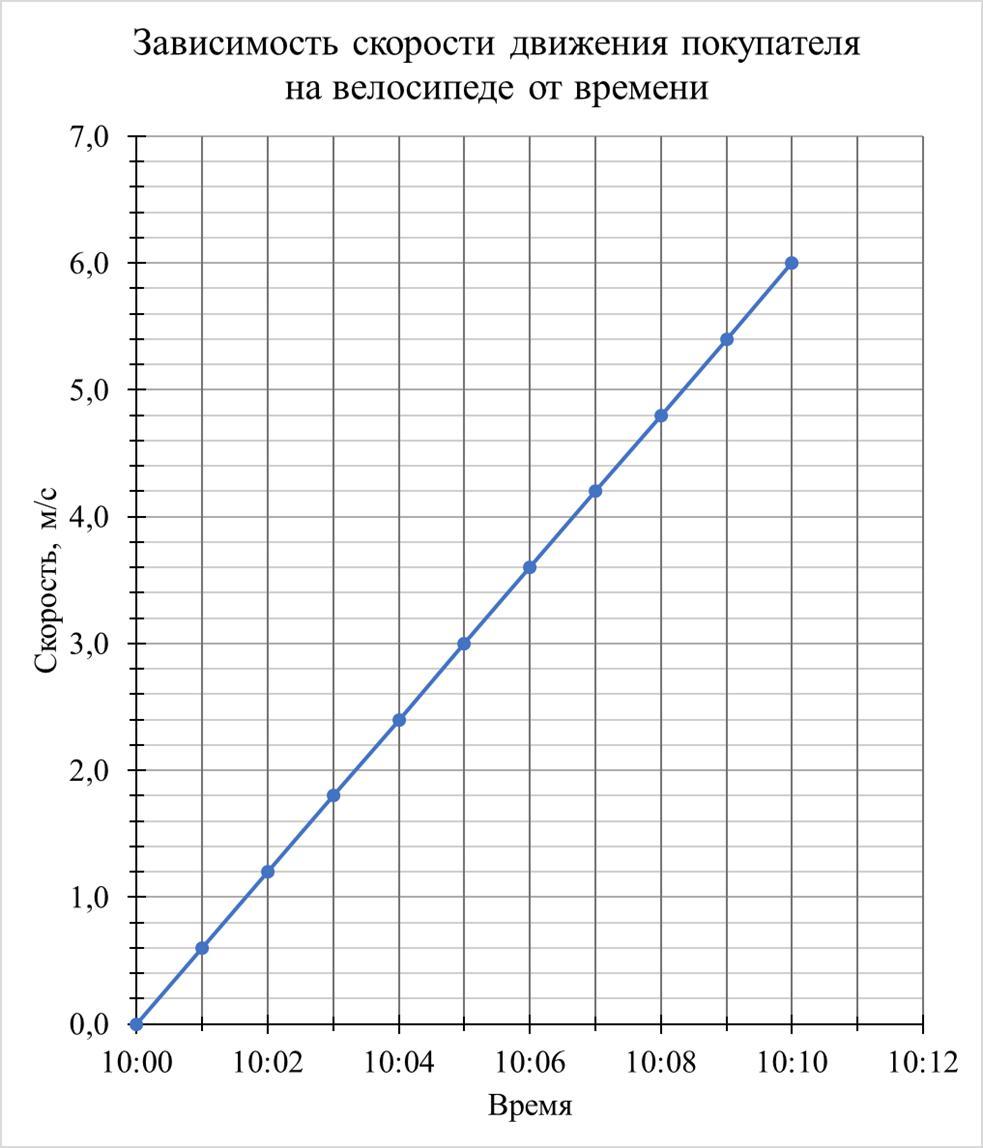
Для проверки достоверности результата я воспользовался графическим калькулятором, чтобы проверить точку пересечения графиков, которые задаются уравнениями движениями людей.

Результат совпадает с требованным, учитывая округления, поэтому ответ достоверный.

Ответ: Администратор должен двигаться с ускорением 0.036 м/с², чтобы догнать покупателя