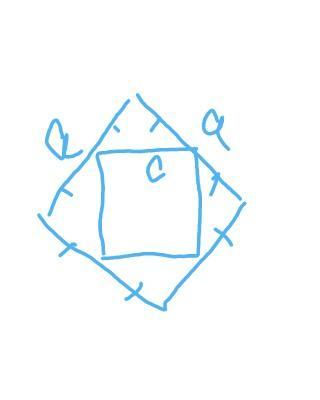
Дан квадрат, вершины которого являются серединами сторон другого квадрата. Определить отношение периметра большего квадрата к периметру меньшего.
С решением пж
siestarjoki:
пусть сторона большего квадрата 2. Тогда сторона меньшего квадрата отсекает прямоугольный равнобедренный треугольник со сторонами 1, 1, √2 (т Пифагора). Периметры квадратов относятся как стороны, 2/√2 =√2
Ответы
Ответ дал:
0
Объяснение:
Периметр большего квадрата :
Р1=4а
Сторона меньшего квадрата равна гипотенузе прямоугольного тр-ка:
Катеты равны а/2
с^2=(а/2)^2+(а/2)^2=(а^2/4)×2=а^2/2
с=а/(корень2)
Р2=4×с=4×а/(корень2)
Р1 : Р2=4а : 4а/(корень2) =
=4а×(корень2) /4а=корень 2
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад