помогите решить эту систему, нужно прямо полное решение
Приложения:
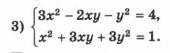
Vopoxov:
У-уфф, либо я как-то по-тупому решал, либо это слегка треш
Ответы
Ответ дал:
1
Ответ:
Объяснение:
Очевидно, что
х = 0 не может быть корнем уравнения
у = 0 не может быть корнем уравнения
поэтому - можно преобразовать уравнение (1) системы после упрощения, разделив обе его части на у²:
Замена переменной:
По Т. Виетта 2 корня:
Делаем обратную замену,
затем выразим х через у:
Решаем уравнение (2)
Решаем уравнение (3)
Подставляем значения, найденные при решении уравнений (2) и (3) - соответственно вместо уравнений (2) и (3)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад