СРОЧНООО! ДАЙЮ 50 БАЛОВ!!!
Знайти область визначення функції y=30/(2-x)²-(2+x)²
Побудувати графік.
Ответы
Ответ дал:
0
Ответ:
Cначала упростим выражение .
Получим функцию .
Знаменатель дроби не равен 0 , поэтому х≠0 и область определения функции - это множество .
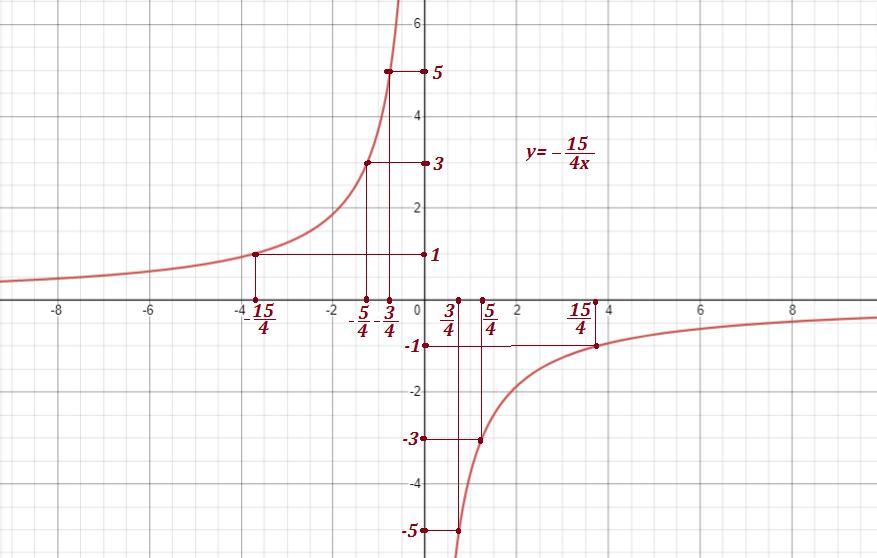
Графиком функции является гипербола, которая проходит через точки с координатами .
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
10 лет назад