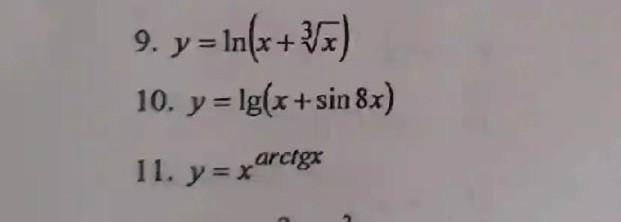Ответы
Ответ дал:
1
Объяснение:
9.
10.
11.
Аноним:
спасибо большое
на другой вопрос тоже посмотрите пожалуйста "производная"
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад