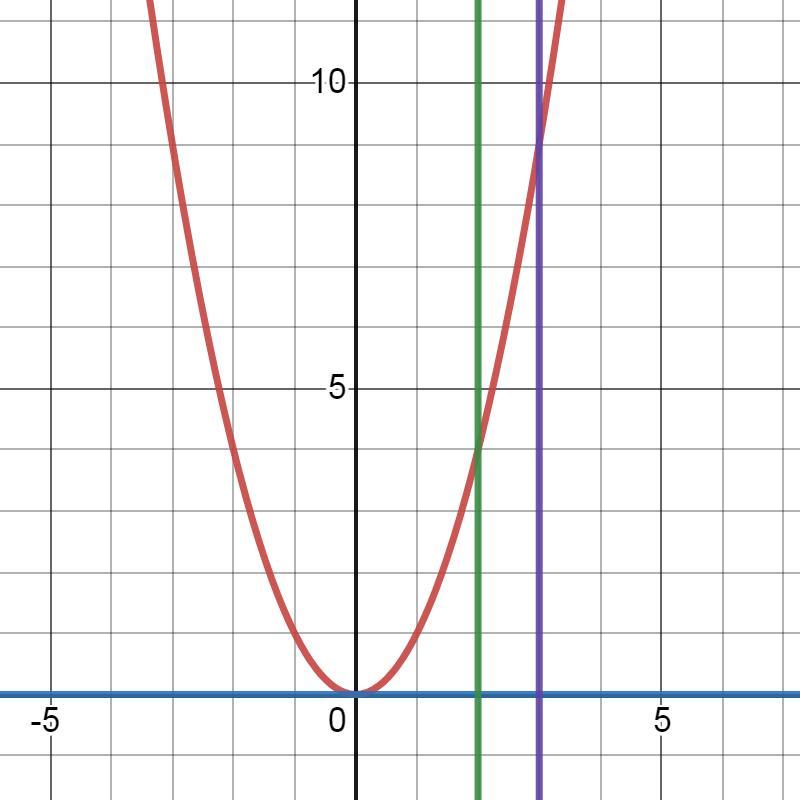
Вычисли площадь S криволинейной трапеции, ограниченной графиком функции f(x)=x ^2 , прямыми y=0 , x=2 и x=3 .
Ответы
Ответ дал:
0
Объяснение:
Ответ: S=6,33333 кв. ед.
Приложения:
masha01021:
помогите пожалуйста
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад