В треугольнике ABC сторона AB вдвое длиннее стороны BC. Найдите, в каком
отношении медианы, проведённые из вершин A и C, делят биссектрису угла B.
Ответы
Ответ дал:
0
Ответ:
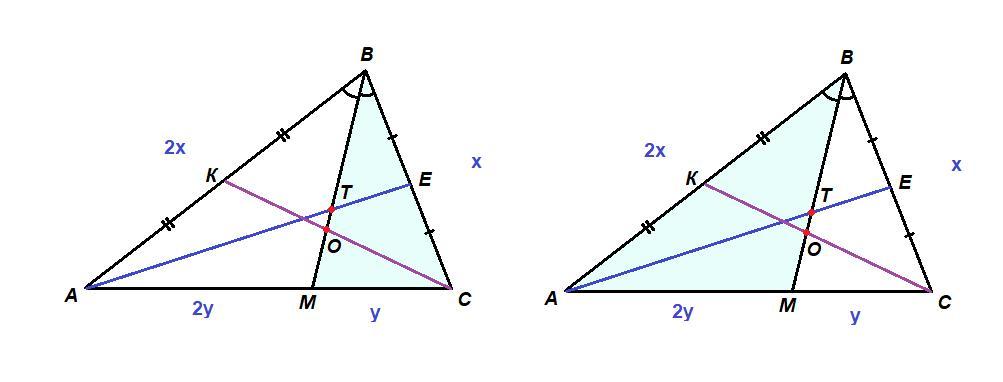
ВТ : ТО : ОМ = 12 : 3 : 5
Пошаговое объяснение:
ВМ - биссектриса угла В.
АЕ и СК - медианы.
АЕ∩ВМ = Т
СК∩ВМ = О
Найти отношение ВТ : ТО : ОМ.
- Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Рассмотрим ΔМВС и секущую АЕ. По теореме Менелая:
Рассмотрим ΔАВМ и секущую СК. По теореме Менелая:
Итак, нашли, какую часть каждый из отрезков ВТ, ТО и ОМ составляет от биссектрисы ВМ.
Осталось привести дроби к общему знаменателю.
ВТ : ТО : ОМ = 12 : 3 : 5
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад