Question

Плоскость a параллельна основанию AD трапеции ABCD и пересекает её боковые стороны в точках M и N. Если AD =17 см, BC =9 см, то найдите длину отрезка MN. Решите пожалуйста!!!​

Answer 1

Ответ:

|MN| = 13 см.

Объяснение:

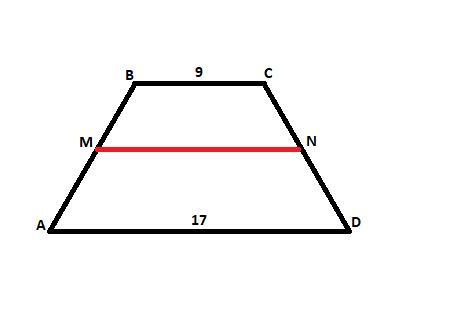
Дана трапеция ABCD, ее основания AD = 17 см, BC = 9 см.

Плоскость трапеции пересекает другая плоскость, параллельная основанию AD, а значит, и параллельная основанию BC.

Найти длину линии пересечения MN.

Решение:

Рисунок я нарисовал.

Если плоскость параллельна основаниям трапеции, то и пересекает она плоскость трапеции по линии, параллельной основаниям.

Поэтому MN || AD || BC.

Пересекать она ее может в любом месте, здесь данных не хватает.

Но мне почему-то кажется, что MN - средняя линия трапеции.

Тогда ее длина:

|MN| = (AD + BC)/2 = (17 + 9)/2 = 13 см