Question

Помогите пожалуйста!! Очень срочно!! Дам 90 баллов!!

Answer 1

Ответ:

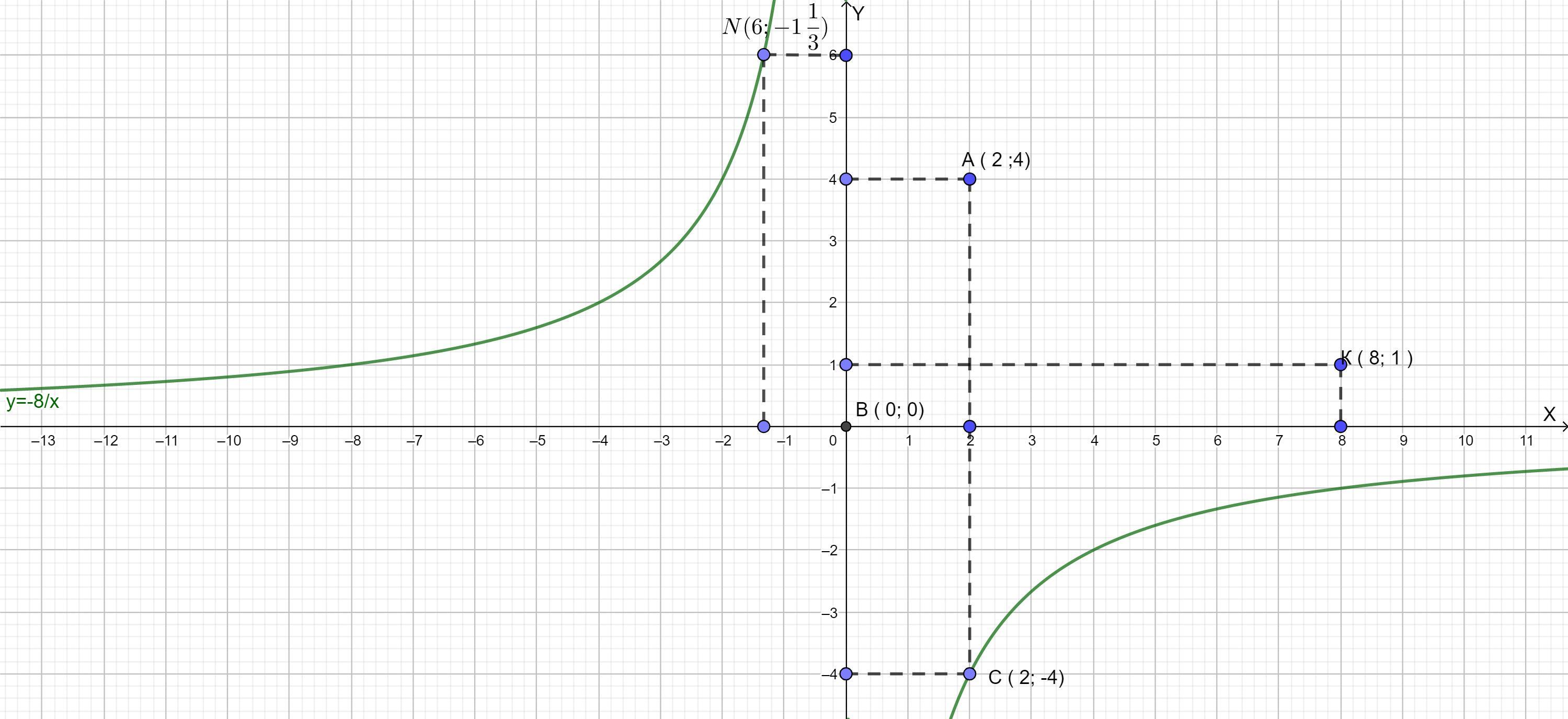
Графику функции во вложении.

а) Если х < 0 , то у > 0.

б) Графику функции y=-8/х принадлежат точки ( 2 ; -4) и

( 6; -1 1/3)

Пошаговое объяснение:

Постройте график функции, заданной формулой у = -8/x. Найдите по графику:

а) каким значениям аргумента х соответствуют положительные значение функции у?

б)какие из точек (2; 4); (0;0); ( 2 ; -4); ( -2; -4); ( 6; -1 1/3); (8; 1) расположены на построенном графике.

Графиком функции y = k x ( k ≠ 0 ) является гипербола, ветви которой находятся в I и III координатных углах при k > 0, и во II и IV координатных углах при k < 0. Точка (0; 0) — центр симметрии гиперболы, оси координат — асимптоты гиперболы.

Построим график функции  у = -8/х . Поскольку k< 0, значит наш график будет находится во II и IV координатных углах.

Составим таблицу значений функции:

$\begin{array}{|c|c|c|c|c|c|c|c|c|}\cline{10- 18} x&-8&-4&-2&-1&1&2&4&8\cline{10-18} y&1&2&4&8&-8&-4&-2&-1 \cline{10-18} \end{array}$

График функции во вложении.

а) Найдем, по графику каким значениям аргумента х соответствуют положительные значение функции у.

По графику видно, что положительным значениям функции у соответствуют отрицательные значения аргумента х.

Если х < 0 , то у > 0

б) Найдем, по графику какие из точек (2; 4); (0;0); ( 2 ; -4); ( -2; -4); ( 6; -1 1/3); (8; 1) расположены на построенном графике.

Точка принадлежит графику функции, если график функции проходит через эту точку.

Отметим эти точки на нашем графике и найдем какие из них принадлежат этому графику.( рисунок 2 во вложении).

Как видим, графику функции y=-8/х принадлежат точки ( 2 ; -4) и

( 6; -1 1/3)