Срочно!!!
Треугольник ABC вписан в окружность. Найдите расстояние от центра этой окружности до стороны AC, если AC=18, а радиус описанной окружности треугольника равен 41.
siestarjoki:
40
Ответы
Ответ дал:
1
Расстояние - кратчайший отрезок - длина перпендикуляра.
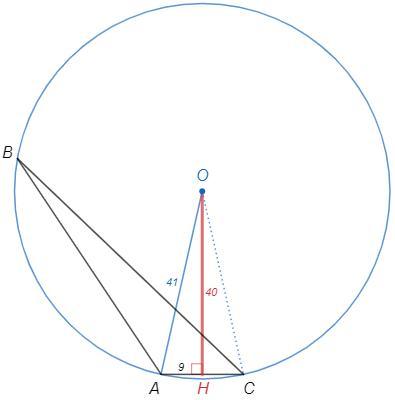
Опустим перпендикуляр OH из центра O к хорде AC.
Перпендикуляр из центра делит хорду пополам.
(OA=OC, радиусы. △AOC - р/б, высота ОН является медианой)
AH=AC/2=18/2=9
△AOH, т Пифагора:
OH =√(OA^2 -AH^2) =√(41^2 -9^2) =40
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад