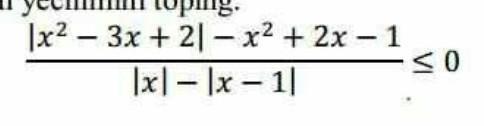Question

Помогите Найти наименьшее натуральное решение задачи ​

Answer 1

Объяснение:

$\frac{|x^2-3x+2|-x^2+2x-1}{|x|-|x-1|}\leq 0\\ 1.\\a) \left \{ {{|x^2-3x+2|-x^2+2x-1\geq 0} \atop {|x|-|x-1| < 0}} \right. \\|x^2-3x+2|-x^2+2x-1\geq 0\\x^2-3x+2\geq 0\\x^2-x-2x+2\geq 0\\x*(x-1)-2*(x-1)\geq 0\\(x-1)*(x-2)\geq 0$

-∞__+__1__-__2__+__+∞

x∈(-∞;1]U[2;+∞).        ⇒

$x^2-3x+2-x^2+2x-1\geq 0\\1-x\geq 0\\x\leq 1.\ \ \ \ \Rightarrow\\x\in(-\infty;1].$

$x^2-3x+2 < 0\\x\in(1;2)\\-x^2+3x-2-x^2+2x-1\geq 0\\-2x^2+5x-3\geq 0\ |*(-1)\\2x^2-5x+3\geq 0\\2x^2-2x-3x+3\geq 0\\2x*(x-1)-3*(x-1)\geq 0\\(x-1)*(2x-3)\geq 0.$

-∞__+__1__-__1,5__+__+∞          ⇒

$x\in(-\infty;1]U[1,5;+\infty)\ \ \ \ \Rightarrow\\x\in[1,5;2).$

$\Rightarrow\ \ \ \ x\in(-\infty;1]U[1,5;2).$

|x|-|x-1|<0

-∞____0____1____+∞

x∈(-∞;0]

-x-(-(x-1))<0

-x+x-1<0

-1<0          ⇒

x∈(-∞;0].

x∈(0;1).

x-(-(x-1)<0

x+x-1<0

2x<1 |:2

x<0,5        ⇒

x∈(0;0,5).

x∈(1;+∞).

x-(x-1)<0

x-x+1<0

1<0  x∈∅.      ⇒

x∈(-∞;0,5).

$\boxed{x\in(-\infty;0,5).}$

$2.\\b)\ \left \{ {{|x^2-3x+2|-x^2+2x-1\leq 0} \atop {|x|-|x-1| > 0}} \right. \\x^2-3x+2\geq 0\\x\in(-\infty;1]U[2;+\infty)\\x^2-3x+2-x^2+2x-1\leq 0\\1-x\leq 0\\x\geq 1\\x\in[2;+\infty)\\x^2-3x+2 < 0\\x\in(1;2).\\-x^2+3x-2-x^2+2x-1\leq 0\\-2x^2+5x-3\leq 0\ |*(-1)\\2x^2-5x+3\leq 0\\x\in[1;1,5].\ \ \ \ \ \Rightarrow\\x\in(\infty;1,5]U[2;+\infty).$

|x|-|x-1|>0

-∞____0____1____+∞

x∈(-∞;0).

-x-(-(x-1)>0

-x+x-1>0

-1>0   x∈∅.

x∈[0;1].

x-(-(x-1)>0

x+x-1>0

2x>1 |:2

x>0,5         ⇒

x∈[0,5;1].

x∈(1;+∞).

x-(x-1)>0

x-x+1>0

1>0      ⇒

x∈(1;+∞)

⇒  x∈(0,5;+∞).

$\boxed{(0,5;+\infty)}.$

x∈(-∞;0,5)U(0,5;+∞).

Ответ: x=1.