Ответы
Ответ дал:
1
Ответ:
Объяснение:
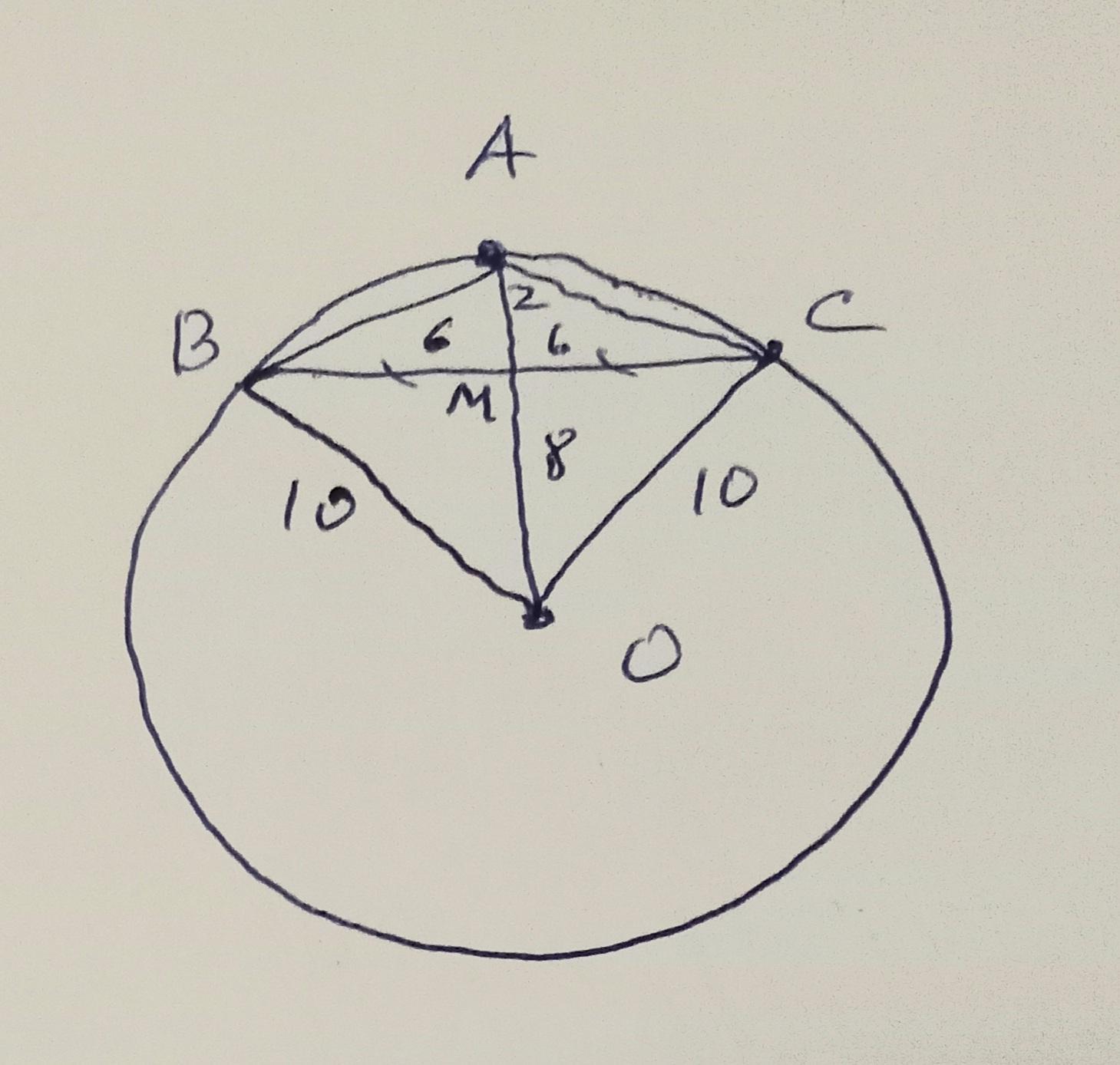
Обозначим точкой М пересечение радиуса АО с отрезком ВС. Треугольники ОМВ равен треугольнику ОМС по трем сторонам: ОМ общая, ОВ = ОС = R, BM = MC по условию. Треугольники прямоугольные, радиус является гипотенузой, а ВМ = МС = ВС/2 = 12/2 = 6
Отсюда ОМ = √(ОВ²-ВМ²) = √(100-36) = 8
Тогда МА = ОА-ОМ = 10-8 = 2
Треугольники МАВ и МАС тоже прямоугольные и также равны по двум сторонам и прямому углу. АВ = АС являются гипотенузами.
АВ = АС = √(ВМ²+МА²) = √(36+4) = √40 = 2√10
Приложения:
ysisk:
Здравствуйте, помогите пожалуйста с вопросом по геометрии на моей странице
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад
