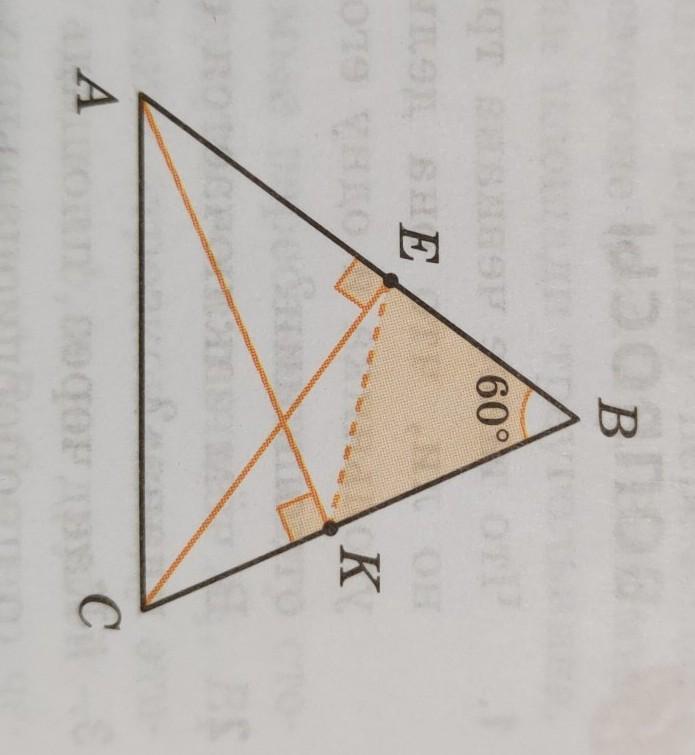
В треугольнике ABC провели высоты АК и CE. Найдите отношение, в котором отрезок ЕК делит площадь треугольника, если угол ABC равен 60°.
Приложения:
Ответы
Ответ дал:
1
Отрезок AC виден из точек E и K под прямым углом - точки A-E-K-C лежат на окружности с диаметром AC.
Четырехугольник AEKC - вписанный, его внешний угол равен противолежащему внутреннему, ∠BKE=∠A.
Треугольники KBE и ABC подобны по углам.
Коэффициент подобия BK/AB=cosB =cos60 =1/2
Площади подобных фигур относятся как квадрат коэффициента подобия, S(KBE)/S(ABC) =1/4
То есть отрезок EK делит площадь треугольника ABC в отношении 1:3
qwer253:
В можете пожалуйста решить без cos?
В треугольнике ABK угол BAK=90-60=30. Катет против угла 30 равен половине гипотенузы, BK=AB/2
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад