Выполнить задание(подробная и чёткая запись):
Приложения:
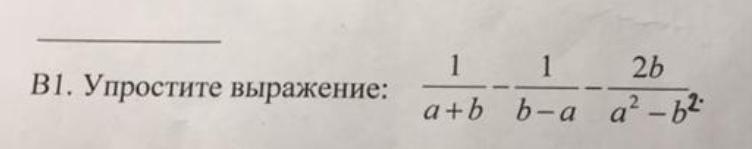
Jomiko:
Ааааа) ясно, добрый человек
Сама не могу,на листочке лучше делать.
ждем ответ от
Fire1ce
Fire1ce
Мне тоже интересно)
Там ещё 3 задания есть.
а вы знаете ответ??
сейчас посчитаю
2/(a+b)
ага
я тоже посчитал
Ответы
Ответ дал:
13
Ответ:
2/(a+b)
Формула:
Пошаговое объяснение:
Вынесем минус за скобки в знаменателе второй дроби и распишем знаменатель третьей дроби по вышеуказанной формуле.
Приведём дроби к общему знаменателю:
Запишем выражение под одним знаменателем и приведём подобные слагаемые:
Вынесем общий множитель в числителе дроби и сократим:
Супер....отличный ответ!
модератор + старший спам аут
Спасибо)
реально..
Ответ дал:
2
Ответ:
2/(a+b)
Пошаговое объяснение:
a²-c²=(a-c)*(a+c)
a²-b²=-(b²-a²)
1/(а+b)-(1/(-(a-b)))-2b/(a²-b²)=
(1/(а+b))+(1/(a-b)-(2b/(a²-b²))=
(а-b+a+b-2b)/(a²-b²)=
2(a-b)/(a²-b²)=
2(a-b)/((a-b)*(a+b))=
2/(a+b)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад