Ответы
Ответ дал:
2
Ответ:
48 кв.см
Объяснение:
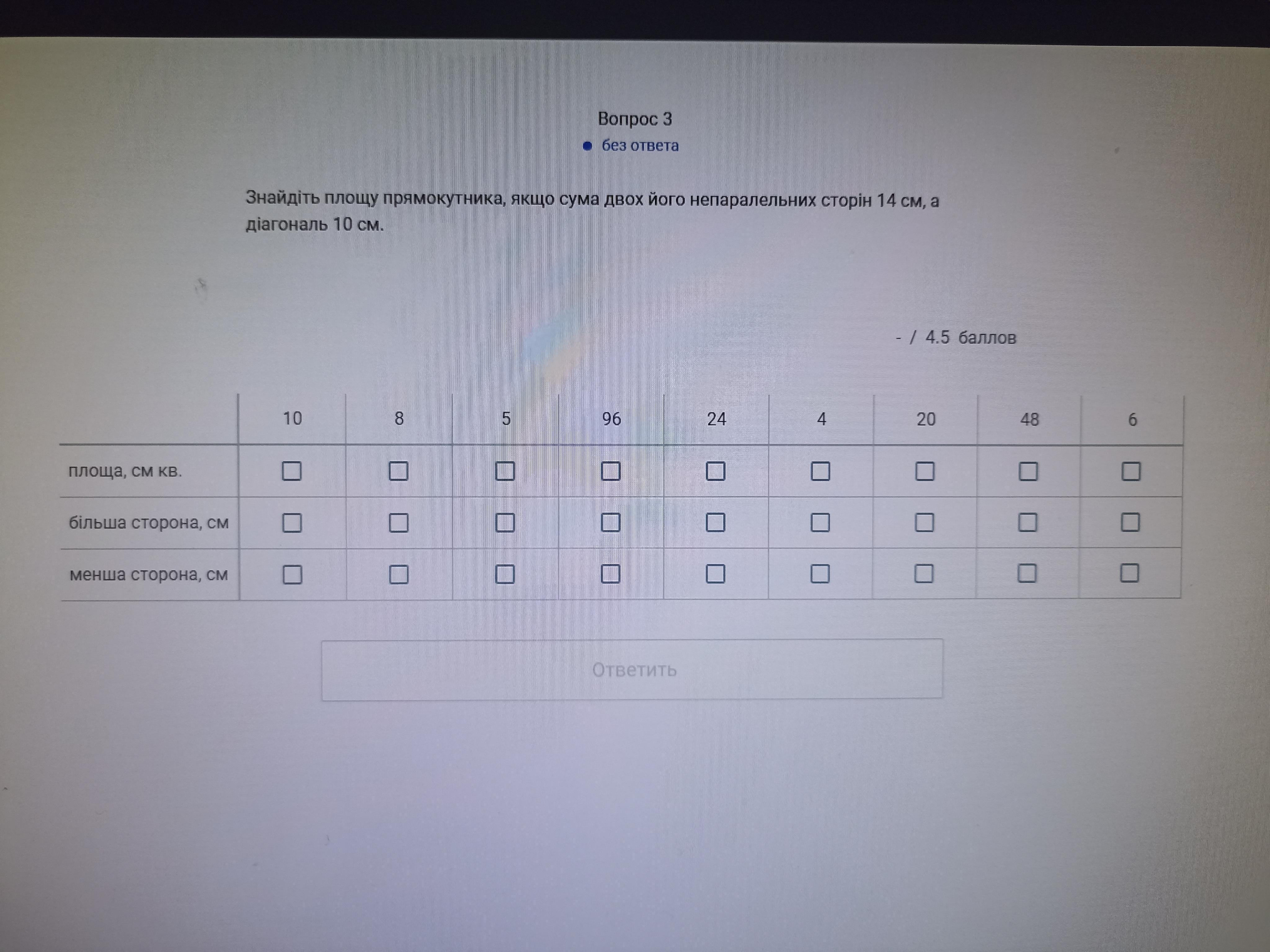
Нехай одна сторона x см (x>0), тодs інша (14-x) см (14-x>0, 14>x). За теоремою Піфагора
( у випадку прямокутника - квадрат діагоналі дорівнює сумі квадратів його непарелельних сторін) складаємо рівняння:
(0<x<14)
|-100
|:2
;
значить сторони прямокутника 8 см і 6 см, тоді площа прямокутника як добуток його двох непаралельних сторін дорівнює
6*8 =48 кв.см
-----------------------------
Нехай одна сторона а см, друга b см. Тоді маємо
- квадрат суми
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад