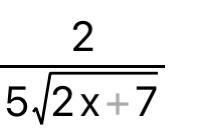Ответы
Ответ дал:
0
Ответ:
Объяснение:
Производная сложной функции:
Ответ дал:
0
Объяснение:
ОТВЕТ: f'(1)=-2/135.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад