Question

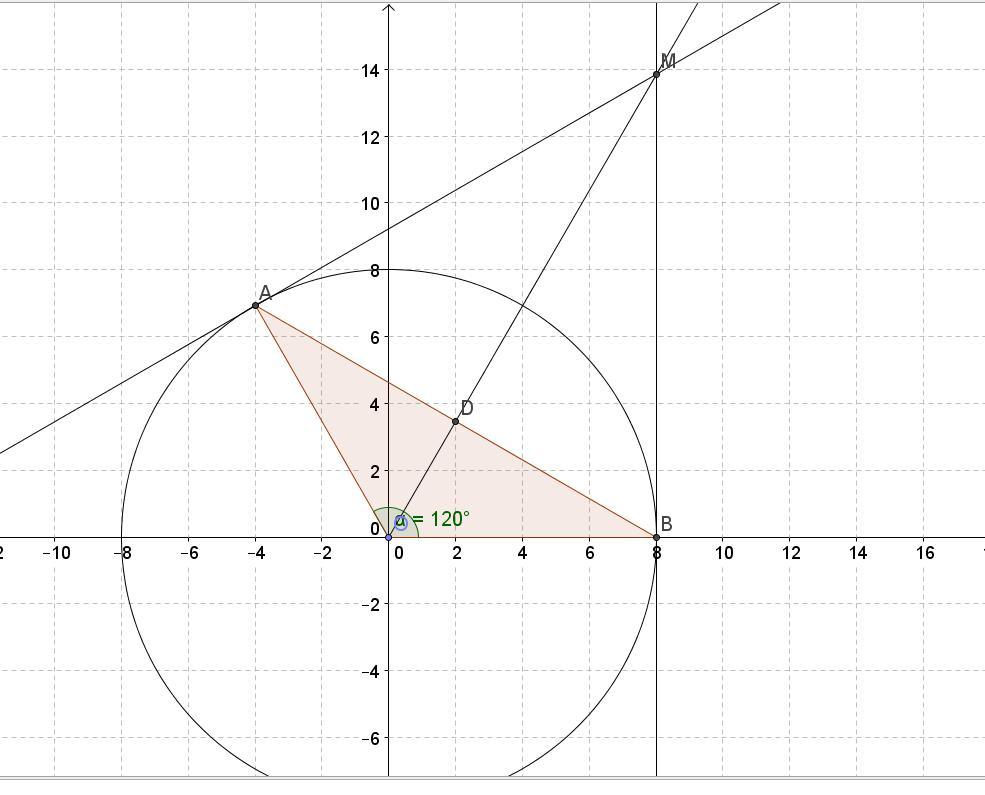
Через точку М к окружности с центром О проведены касательные АМ и ВМ (А и В – точки касания). Известно, что ОМ = 16 см, ∠AOB=120 ∘ .
Найдите диаметр окружности. (В ответе запишите только число, без единиц измерения.)

Answer 1

Сумма углов четырёхугольника ОАМВ равна 360 градусов.

Из них 2 - прямые а точках касания.

Угол АМВ = 360 - 2*90 - 120 = 60 градусов.

Отрезок ОМ делит его пополам.

Радиус окружности R = 16*sin 30° = 16*(1/2) = 8 см.

Ответ: диаметр окружности D = 2R = 2*8 = 16 см.