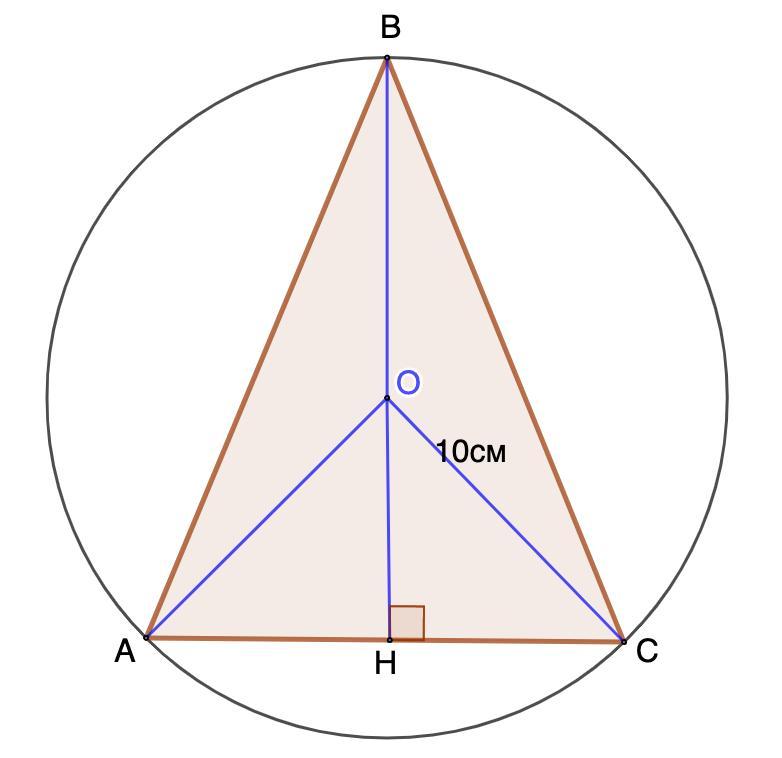
Найдите стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна 16 см, а радиус окружности, в которую он вписан 10 см.
Ответы
Ответ:
Стороны остроугольного равнобедренного треугольника равны:
АС = 16 см; АВ = ВС = 8√5 см
Объяснение:
Найти стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна 16 см, а радиус окружности, в которую он вписан 10 см.
Дано: ΔАВС - равнобедренный;
ВН = 16 см - высота;
Окр.О,R - описанная;
R = 10 см.
Найти: АВ; ВС; АС.
Решение:
Проведем радиусы ОА и ОС.
1. Рассмотрим ΔАОС.
ОА = ОС = R
⇒ ΔАОС - равнобедренный.
ОН - высота.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
⇒ ОН - медиана.
2. Рассмотрим ΔНОС - прямоугольный.
ОС = 10 см; ОН = ВН - ОВ = 16 - 10 = 6 см;
По теореме Пифагора:
НС² = ОС² - ОН² = 100 - 36 = 64
НС = √64 = 8 (см)
⇒ АС = 8 · 2 = 16 (см)
3. Рассмотрим ΔНВС - прямоугольный.
По теореме Пифагора:
ВС² = ВН² + НС² = 64 + 256 = 320
ВС = 8√5 (см)
⇒ АВ = ВС = 8√5 см