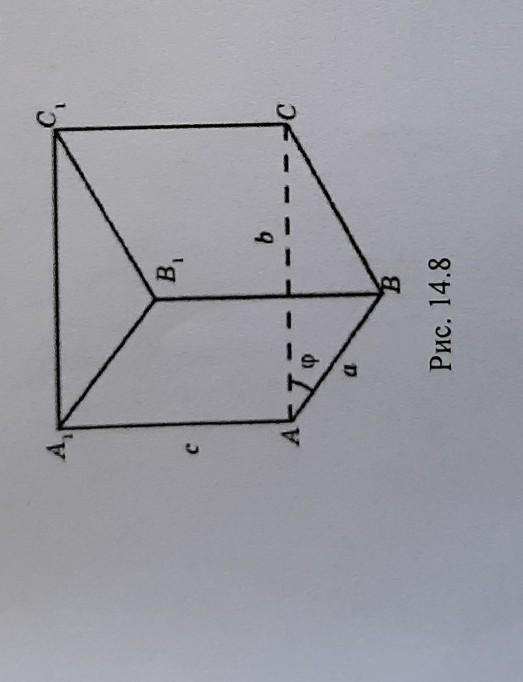
a и b - стороны основания прямой треугольной призмы, ф - угол между ними, а c - боковое ребро призмы: a=2 см, b=23 см, ф= 60°, c=5 см. Найти площади её боковой и полной поверхностей.
рисунок чуть кривой сорян ;(
Приложения:
Ответы
Ответ дал:
2
Решение.
Площадь боковой поверхности призмы равно сумме площадей боковых граней, которые являются прямоугольниками.
S(AA₁B₁B) = a*c = 2*5 = 10 (cм²)
S(AA₁C₁C) = b*c = 23*5 = 115 (cм²)
Чтобы найти сторону ВС основания, применим теорему косинусов.
Площадь боковой поверхности призмы равна
(см²)
Площадь основания
(см²)
Таких оснований два, поэтому площадь обоих оснований равна см² .
Полная поверхность S(полн.) = (см²) .
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад